Refine listing
Actions for selected content:
156 results in 13Dxx
de Rham cohomology of local cohomology modules: The graded case
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-21
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Mixed motivic sheaves (and weights for them) exist if ‘ordinary’ mixed motives do
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 917-956
- Print publication:
- May 2015
-
- Article
- Export citation
VANISHING OF COHOMOLOGY OVER COMPLETE INTERSECTION RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 445-455
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
PRO CDH-DESCENT FOR CYCLIC HOMOLOGY AND
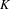 $K$-THEORY
$K$-THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 27 November 2014, pp. 539-567
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
Relation between two twisted inverse image pseudofunctors in duality theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 19 November 2014, pp. 735-764
- Print publication:
- April 2015
-
- Article
- Export citation
DERIVED LOGARITHMIC GEOMETRY I
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 28 October 2014, pp. 367-405
- Print publication:
- April 2016
-
- Article
- Export citation
Koszul Complexes and Pole Order Filtrations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 333-354
-
- Article
-
- You have access
- Export citation
Corrigendum: Filtering free resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1482-1484
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Hopfological algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1-45
- Print publication:
- January 2014
-
- Article
- Export citation
BALANCE FOR TATE COHOMOLOGY WITH RESPECT TO SEMIDUALIZING MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 223-240
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Cohomological and projective dimensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 1203-1210
- Print publication:
- July 2013
-
- Article
- Export citation
SOME ISOMORPHISMS IN DERIVED FUNCTORS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 15 May 2013, pp. 222-233
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Filtering free resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 18 March 2013, pp. 754-772
- Print publication:
- May 2013
-
- Article
- Export citation
ON A CLASS OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 514-526
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
THE TOP LEFT DERIVED FUNCTORS OF THE GENERALISED
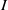 $I$-ADIC COMPLETION
$I$-ADIC COMPLETION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 04 January 2013, pp. 259-266
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
LOCAL-GLOBAL PRINCIPLE FOR THE FINITENESS AND ARTINIANNESS OF GENERALISED LOCAL COHOMOLOGY MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 20 August 2012, pp. 480-492
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Hilbert schemes and Betti numbers over Clements–Lindström rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1337-1364
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Freeness and multirestriction of hyperplane arrangements
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 22 March 2012, pp. 799-806
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Picard groups of punctured spectra of dimension three local hypersurfaces are torsion-free
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 145-152
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Cotorsion pairs and model structures on Ch(R)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 17 August 2011, pp. 783-797
-
- Article
-
- You have access
- Export citation
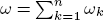 . Let
. Let 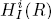 are holonomic (
are holonomic (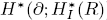 are concentrated in degree —
are concentrated in degree —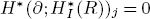 for
for 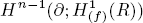 to
to 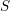
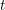
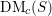
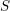
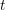
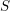
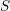
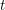
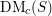
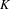
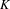
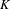
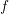
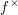
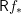
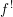
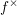
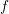
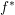
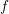
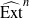
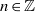
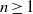


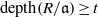

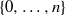
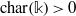
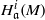
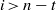
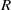
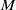
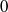
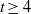
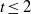
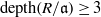
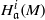
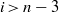
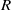
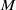
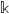
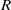
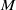
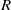

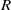
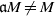

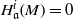
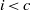
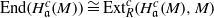

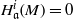
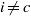
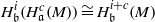
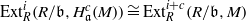
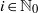
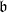
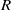
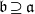

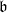
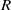
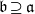
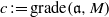
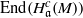
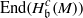
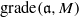
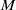

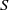
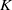
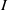
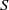
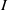
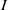
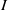
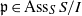
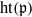
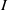
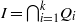
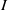
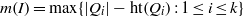
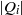
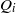
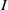
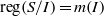
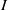
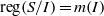
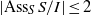
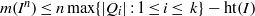
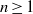
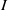
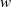
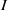
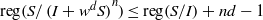
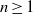
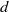
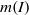
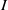
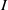
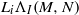
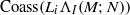
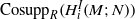
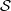
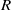
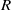

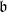
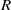
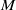
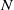
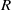
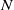
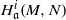
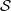
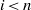
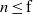
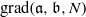
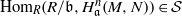
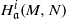
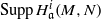
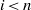
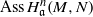
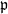
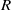
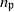
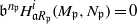
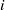


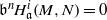

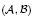 in the category of modules is complete and hereditary, then both of the induced cotorsion pairs in the category of complexes are complete. We also give a cofibrantly generated model structure that can be regarded as a generalization of the projective model structure.
in the category of modules is complete and hereditary, then both of the induced cotorsion pairs in the category of complexes are complete. We also give a cofibrantly generated model structure that can be regarded as a generalization of the projective model structure.