Consider a sequence (X k : k ≥ 0) of regularly varying independent and identically distributed random variables with mean 0 and finite variance. We develop efficient rare-event simulation methodology associated with large deviation probabilities for the random walk (S n : n ≥ 0). Our techniques are illustrated by examples, including large deviations for the empirical mean and path-dependent events. In particular, we describe two efficient state-dependent importance sampling algorithms for estimating the tail of S n in a large deviation regime as n ↗ ∞. The first algorithm takes advantage of large deviation approximations that are used to mimic the zero-variance change of measure. The second algorithm uses a parametric family of changes of measure based on mixtures. Lyapunov-type inequalities are used to appropriately select the mixture parameters in order to guarantee bounded relative error (or efficiency) of the estimator. The second example involves a path-dependent event related to a so-called knock-in financial option under heavy-tailed log returns. Again, the importance sampling algorithm is based on a parametric family of mixtures which is selected using Lyapunov bounds. In addition to the theoretical analysis of the algorithms, numerical experiments are provided in order to test their empirical performance.

We build a family of Markov chains on a sphere using distance-based long-range connection probabilities to model the decentralized message-passing problem that has recently gained significant attention in the small-world literature. Starting at an arbitrary source point on the sphere, the expected message delivery time to an arbitrary target on the sphere is characterized by a particular expected hitting time of our Markov chains. We prove that, within this family, there is a unique efficient Markov chain whose expected hitting time is polylogarithmic in the relative size of the sphere. For all other chains, this expected hitting time is at least polynomial. We conclude by defining two structural properties, called scale invariance and steady improvement, of the probability density function of long-range connections and prove that they are sufficient and necessary for efficient decentralized message delivery.

We analyze the unit-demand Euclidean vehicle routeing problem, where n customers are modeled as independent, identically distributed uniform points and have unit demand. We show new lower bounds on the optimal cost for the metric vehicle routeing problem and analyze them in this setting. We prove that there exists a constant ĉ > 0 such that the iterated tour partitioning heuristic given by Haimovich and Rinnooy Kan (1985) is a (2 - ĉ)-approximation algorithm with probability arbitrarily close to 1 as the number of customers goes to ∞. It has been a longstanding open problem as to whether one can improve upon the factor of 2 given by Haimovich and Rinnooy Kan. We also generalize this, and previous results, to the multidepot case.

In a recent paper, Kleinberg (2000) considered a small-world network model consisting of a d-dimensional lattice augmented with shortcuts. The probability of a shortcut being present between two points decays as a power, r -α, of the distance, r, between them. Kleinberg showed that greedy routeing is efficient if α = d and that there is no efficient decentralised routeing algorithm if α ≠ d. The results were extended to a continuum model by Franceschetti and Meester (2003). In our work, we extend the result to more realistic models constructed from a Poisson point process wherein each point is connected to all its neighbours within some fixed radius, and possesses random shortcuts to more distant nodes as described above.

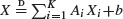In this paper we consider stochastic recursive equations of sum type, , and of max type, 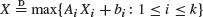, where 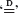A i , b i , and b are random, (X i ) are independent, identically distributed copies of X, and denotes equality in distribution. Equations of these types typically characterize limits in the probabilistic analysis of algorithms, in combinatorial optimization problems, and in many other problems having a recursive structure. We develop some new contraction properties of minimal L s -metrics which allow us to establish general existence and uniqueness results for solutions without imposing any moment conditions. As an application we obtain a one-to-one relationship between the set of solutions to the homogeneous equation and the set of solutions to the inhomogeneous equation, for sum- and max-type equations. We also give a stochastic interpretation of a recent transfer principle of Rösler from nonnegative solutions of sum type to those of max type, by means of random scaled Weibull distributions.

Consider a countable list of files updated according to the move-to-front rule. Files have independent random weights, which are used to construct request probabilities. Exact and asymptotic formulae for the Laplace transform of the stationary search cost are given for i.i.d. weights. Similar expressions are derived for the first two moments. Some results are extended to the case of independent weights.

We investigate the limit distributions associated with cost measures in Sattolo's algorithm for generating random cyclic permutations. The number of moves made by an element turns out to be a mixture of 1 and 1 plus a geometric distribution with parameter ½, where the mixing probability is the limiting ratio of the rank of the element being moved to the size of the permutation. On the other hand, the raw distance traveled by an element to its final destination does not converge in distribution without norming. Linearly scaled, the distance converges to a mixture of a uniform and a shifted product of a pair of independent uniforms. The results are obtained via randomization as a transform, followed by derandomization as an inverse transform. The work extends analysis by Prodinger.