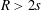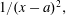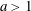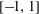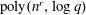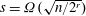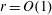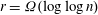Refine listing
Actions for selected content:
84 results in 68Wxx
A spectral method for community detection in moderately sparse degree-corrected stochastic block models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 686-721
- Print publication:
- September 2017
-
- Article
- Export citation
THE SHORT RESOLUTION OF A SEMIGROUP ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 400-411
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
GPU-Accelerated LOBPCG Method with Inexact Null-Space Filtering for Solving Generalized Eigenvalue Problems in Computational Electromagnetics Analysis with Higher-Order FEM
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 4 / October 2017
- Published online by Cambridge University Press:
- 28 July 2017, pp. 997-1014
- Print publication:
- October 2017
-
- Article
- Export citation
Convex Polygons in Geometric Triangulations†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 30 May 2017, pp. 641-659
-
- Article
- Export citation
PyCFTBoot: A Flexible Interface for the Conformal Bootstrap
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 1-38
- Print publication:
- July 2017
-
- Article
- Export citation
Delaunay Graph Based Inverse Distance Weighting for Fast Dynamic Meshing
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 27 March 2017, pp. 1282-1309
- Print publication:
- May 2017
-
- Article
- Export citation
From coin tossing to rock-paper-scissors and beyond: a log-exp gap theorem for selecting a leader
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 213-235
- Print publication:
- March 2017
-
- Article
- Export citation
A Robust and Efficient Adaptive Multigrid Solver for the Optimal Control of Phase Field Formulations of Geometric Evolution Laws
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 65-92
- Print publication:
- January 2017
-
- Article
- Export citation
New Non-Travelling Wave Solutions of Calogero Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 1036-1049
- Print publication:
- December 2016
-
- Article
- Export citation
An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without a low-level encoding of zero
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 255-266
-
- Article
-
- You have access
- Export citation
Direct Gravitational Search Algorithm for Global Optimisation Problems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 290-313
- Print publication:
- August 2016
-
- Article
- Export citation
Efficient Implementation of Smoothed Particle Hydrodynamics (SPH) with Plane Sweep Algorithm
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 770-800
- Print publication:
- March 2016
-
- Article
- Export citation
The Multiple-Orientability Thresholds for Random Hypergraphs†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 28 December 2015, pp. 870-908
-
- Article
- Export citation
Multivariate Distributions with Fixed Marginals and Correlations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 602-608
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
A Binomial Splitting Process in Connection with Corner Parking Problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 971-989
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A study of the representations supported by the orbit closure of the determinant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 292-312
- Print publication:
- February 2015
-
- Article
- Export citation
Approximating the densest sublattice from Rankin’s inequality
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 92-111
-
- Article
-
- You have access
- Export citation
Rational functions with maximal radius of absolute monotonicity
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 159-205
-
- Article
-
- You have access
- Export citation
A note on uniform approximation of functions having a double pole
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 233-244
-
- Article
-
- You have access
- Export citation
Deterministic polynomial factoring and association schemes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 123-140
-
- Article
-
- You have access
- Export citation
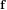

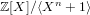
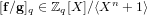
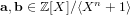
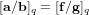
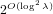
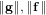
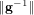

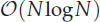 neighbour search method based on the plane sweep (PW) algorithm with
neighbour search method based on the plane sweep (PW) algorithm with