We study the geometry underlying the difference between non-negative polynomials and sums of squares (SOS). The hypersurfaces that discriminate these two cones for ternary sextics and quaternary quartics are shown to be Noether–Lefschetz loci of K3 surfaces. The projective duals of these hypersurfaces are defined by rank constraints on Hankel matrices. We compute their degrees using numerical algebraic geometry, thereby verifying results due to Maulik and Pandharipande. The non-SOS extreme rays of the two cones of non-negative forms are parametrized, respectively, by the Severi variety of plane rational sextics and by the variety of quartic symmetroids.

Estimator algorithms in learning automata are useful tools for adaptive, real-time optimization in computer science and engineering applications. In this paper we investigate theoretical convergence properties for a special case of estimator algorithms - the pursuit learning algorithm. We identify and fill a gap in existing proofs of probabilistic convergence for pursuit learning. It is tradition to take the pursuit learning tuning parameter to be fixed in practical applications, but our proof sheds light on the importance of a vanishing sequence of tuning parameters in a theoretical convergence analysis.

A navigation on a set of points S is a rule for choosing which point to move to from the present point in order to progress toward a specified target. We study some navigations in the plane where S is a nonuniform Poisson point process (in a finite domain) with intensity going to +∞. We show the convergence of the traveller's path lengths, and give the number of stages and the geometry of the traveller's trajectories, uniformly for all starting points and targets, for several navigations of geometric nature. Other costs are also considered. This leads to asymptotic results on the stretch factors of random Yao graphs and random θ-graphs.

In 1992, Göran Björck and Ralf Fröberg completely characterized the solution set of cyclic-8. In 2001, Jean-Charles Faugère determined the solution set of cyclic-9, by computer algebra methods and Gröbner basis computation. In this paper, a new theory in matrix analysis of rank-deficient matrices together with algorithms in numerical algebraic geometry enables us to present a symbolic-numerical algorithm to derive exactly the defining polynomials of all prime ideals of positive dimension in primary decomposition of cyclic-12. Empirical evidence together with rigorous proof establishes the fact that the positive-dimensional solution variety of cyclic-12 just consists of 72 quadrics of dimension one.

We consider a serialized coin-tossing leader election algorithm that proceeds in rounds until a winner is chosen, or all contestants are eliminated. The analysis allows for either biased or fair coins. We find the exact distribution for the duration of any fixed contestant; asymptotically, it turns out to be a geometric distribution. Rice's method (an analytic technique) shows that the moments of the duration contain oscillations, which we give explicitly for the mean and variance. We also use convergence in the Wasserstein metric space to show that the distribution of the total number of coin flips (among all participants), suitably normalized, approaches a normal limiting random variable.

In this paper we study the number of random records in an arbitrary split tree (or, equivalently, the number of random cuttings required to eliminate the tree). We show that a classical limit theorem for the convergence of sums of triangular arrays to infinitely divisible distributions can be used to determine the distribution of this number. After normalization the distributions are shown to be asymptotically weakly 1-stable. This work is a generalization of our earlier results for the random binary search tree in Holmgren (2010), which is one specific case of split trees. Other important examples of split trees include m-ary search trees, quad trees, medians of (2k + 1)-trees, simplex trees, tries, and digital search trees.

We introduce a formal limit, which we refer to as a fluid limit, of scaled stochastic models for a cache managed with the least-recently-used algorithm when requests are issued according to general stochastic point processes. We define our fluid limit as a superposition of dependent replications of the original system with smaller item sizes when the number of replications approaches ∞. We derive the average probability that a requested item is not in a cache (average miss probability) in the fluid limit. We show that, when requests follow inhomogeneous Poisson processes, the average miss probability in the fluid limit closely approximates that in the original system. Also, we compare the asymptotic characteristics, as the cache size approaches ∞, of the average miss probability in the fluid limit to those in the original system.

We consider the problem of efficient estimation via simulation of first passage time probabilities for a multidimensional random walk with heavy-tailed increments. In addition to being a natural generalization to the problem of computing ruin probabilities in insurance - in which the focus is the maximum of a one-dimensional random walk with negative drift - this problem captures important features of large deviations for multidimensional heavy-tailed processes (such as the role played by the mean of the process in connection to the location of the target set). We develop a state-dependent importance sampling estimator for this class of multidimensional problems. Then, using techniques based on Lyapunov inequalities, we argue that our estimator is strongly efficient in the sense that the relative mean squared error of our estimator can be made arbitrarily small by increasing the number of replications, uniformly as the probability of interest approaches 0.

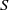
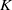
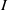
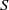
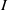
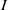
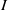
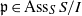
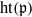
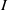
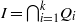
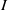
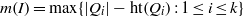
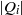
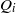
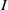
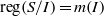
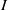
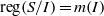
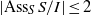
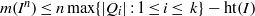
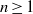
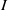
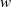
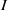
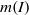
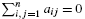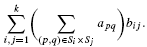
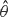In the kernel clustering problem we are given a large n × n positive-semidefinite matrix A = (aij) with and a small k × k positive-semidefinite matrix B = (bij). The goal is to find a partition S1, …, Sk of {1, … n} which maximizes the quantity

We study the computational complexity of this generic clustering problem which originates in the theory of machine learning. We design a constant factor polynomial time approximation algorithm for this problem, answering a question posed by Song et al. In some cases we manage to compute the sharp approximation threshold for this problem assuming the unique games conjecture (UGC). In particular, when B is the 3 × 3 identity matrix the UGC hardness threshold of this problem is exactly 16π/27. We present and study a geometric conjecture of independent interest which we show would imply that the UGC threshold when B is the k × k identity matrix is (8π/9)(1 – 1/k) for every k ≥ 3.

The standard Markov chain Monte Carlo method of estimating an expected value is to generate a Markov chain which converges to the target distribution and then compute correlated sample averages. In many applications the quantity of interest θ is represented as a product of expected values, θ = µ1 ⋯ µk, and a natural estimator is a product of averages. To increase the confidence level, we can compute a median of independent runs. The goal of this paper is to analyze such an estimator , i.e. an estimator which is a ‘median of products of averages’ (MPA). Sufficient conditions are given for 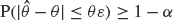to have fixed relative precision at a given level of confidence, that is, to satisfy . Our main tool is a new bound on the mean-square error, valid also for nonreversible Markov chains on a finite state space.

We study a process where balls are repeatedly thrown into n boxes independently according to some probability distribution p. We start with n balls, and at each step, all balls landing in the same box are fused into a single ball; the process terminates when there is only one ball left (coalescence). Let c := ∑jpj2, the collision probability of two fixed balls. We show that the expected coalescence time is asymptotically 2c−1, under two constraints on p that exclude a thin set of distributions p. One of the constraints is c = o(ln−2n). This ln−2n is shown to be a threshold value: for c = ω(ln−2n), there exists p with c(p) = c such that the expected coalescence time far exceeds c−1. Connections to coalescent processes in population biology and theoretical computer science are discussed.

Consider a sequence (Xk: k ≥ 0) of regularly varying independent and identically distributed random variables with mean 0 and finite variance. We develop efficient rare-event simulation methodology associated with large deviation probabilities for the random walk (Sn: n ≥ 0). Our techniques are illustrated by examples, including large deviations for the empirical mean and path-dependent events. In particular, we describe two efficient state-dependent importance sampling algorithms for estimating the tail of Sn in a large deviation regime as n ↗ ∞. The first algorithm takes advantage of large deviation approximations that are used to mimic the zero-variance change of measure. The second algorithm uses a parametric family of changes of measure based on mixtures. Lyapunov-type inequalities are used to appropriately select the mixture parameters in order to guarantee bounded relative error (or efficiency) of the estimator. The second example involves a path-dependent event related to a so-called knock-in financial option under heavy-tailed log returns. Again, the importance sampling algorithm is based on a parametric family of mixtures which is selected using Lyapunov bounds. In addition to the theoretical analysis of the algorithms, numerical experiments are provided in order to test their empirical performance.

We build a family of Markov chains on a sphere using distance-based long-range connection probabilities to model the decentralized message-passing problem that has recently gained significant attention in the small-world literature. Starting at an arbitrary source point on the sphere, the expected message delivery time to an arbitrary target on the sphere is characterized by a particular expected hitting time of our Markov chains. We prove that, within this family, there is a unique efficient Markov chain whose expected hitting time is polylogarithmic in the relative size of the sphere. For all other chains, this expected hitting time is at least polynomial. We conclude by defining two structural properties, called scale invariance and steady improvement, of the probability density function of long-range connections and prove that they are sufficient and necessary for efficient decentralized message delivery.

We analyze the unit-demand Euclidean vehicle routeing problem, where n customers are modeled as independent, identically distributed uniform points and have unit demand. We show new lower bounds on the optimal cost for the metric vehicle routeing problem and analyze them in this setting. We prove that there exists a constant ĉ > 0 such that the iterated tour partitioning heuristic given by Haimovich and Rinnooy Kan (1985) is a (2 - ĉ)-approximation algorithm with probability arbitrarily close to 1 as the number of customers goes to ∞. It has been a longstanding open problem as to whether one can improve upon the factor of 2 given by Haimovich and Rinnooy Kan. We also generalize this, and previous results, to the multidepot case.

In a recent paper, Kleinberg (2000) considered a small-world network model consisting of a d-dimensional lattice augmented with shortcuts. The probability of a shortcut being present between two points decays as a power, r-α, of the distance, r, between them. Kleinberg showed that greedy routeing is efficient if α = d and that there is no efficient decentralised routeing algorithm if α ≠ d. The results were extended to a continuum model by Franceschetti and Meester (2003). In our work, we extend the result to more realistic models constructed from a Poisson point process wherein each point is connected to all its neighbours within some fixed radius, and possesses random shortcuts to more distant nodes as described above.

In this paper we consider stochastic recursive equations of sum type, , and of max type, , where Ai, bi, and b are random, (Xi) are independent, identically distributed copies of X, and denotes equality in distribution. Equations of these types typically characterize limits in the probabilistic analysis of algorithms, in combinatorial optimization problems, and in many other problems having a recursive structure. We develop some new contraction properties of minimal Ls-metrics which allow us to establish general existence and uniqueness results for solutions without imposing any moment conditions. As an application we obtain a one-to-one relationship between the set of solutions to the homogeneous equation and the set of solutions to the inhomogeneous equation, for sum- and max-type equations. We also give a stochastic interpretation of a recent transfer principle of Rösler from nonnegative solutions of sum type to those of max type, by means of random scaled Weibull distributions.

Consider a countable list of files updated according to the move-to-front rule. Files have independent random weights, which are used to construct request probabilities. Exact and asymptotic formulae for the Laplace transform of the stationary search cost are given for i.i.d. weights. Similar expressions are derived for the first two moments. Some results are extended to the case of independent weights.

We investigate the limit distributions associated with cost measures in Sattolo's algorithm for generating random cyclic permutations. The number of moves made by an element turns out to be a mixture of 1 and 1 plus a geometric distribution with parameter ½, where the mixing probability is the limiting ratio of the rank of the element being moved to the size of the permutation. On the other hand, the raw distance traveled by an element to its final destination does not converge in distribution without norming. Linearly scaled, the distance converges to a mixture of a uniform and a shifted product of a pair of independent uniforms. The results are obtained via randomization as a transform, followed by derandomization as an inverse transform. The work extends analysis by Prodinger.