Refine listing
Actions for selected content:
326 results in 52Axx
On maximal simplices inscribed in a central convex set
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 38-44
- Print publication:
- June 1974
-
- Article
- Export citation
A lattice problem in the plane
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-252
- Print publication:
- December 1973
-
- Article
- Export citation
The convex generation of convex Borel sets in Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-3
- Print publication:
- June 1973
-
- Article
- Export citation
An integral-geometric meaning for lower order area functions of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-212
- Print publication:
- December 1972
-
- Article
- Export citation
Symmetrical sets of constant width and their partitions
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-111
- Print publication:
- June 1971
-
- Article
- Export citation
A convex body with a false centre is an ellipsoid
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-59
- Print publication:
- June 1971
-
- Article
- Export citation
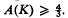 . We prove here a result in the opposite direction.
. We prove here a result in the opposite direction.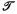 is made up of all those figures from a certain class which support, in some sense, a convex body. Further, the examples lead us to expect that measures of this kind will appear as integrals of densities which may depend on the choices of
is made up of all those figures from a certain class which support, in some sense, a convex body. Further, the examples lead us to expect that measures of this kind will appear as integrals of densities which may depend on the choices of 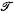 . Here we treat a question of the type just described: to determine a measure for sets of
. Here we treat a question of the type just described: to determine a measure for sets of 