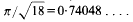Refine listing
Actions for selected content:
326 results in 52Axx
Maximal sections and centrally symmetric bodies
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 19-30
- Print publication:
- December 2000
-
- Article
- Export citation
Inscribing cubes and covering by rhombic dodecahedra via equivariant topology
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 371-397
- Print publication:
- December 2000
-
- Article
- Export citation
On the LLN for the number of vertices of a random convex hull
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 675-681
- Print publication:
- September 2000
-
- Article
- Export citation
Systematic sampling on the circle and on the sphere
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 628-647
- Print publication:
- September 2000
-
- Article
- Export citation
Poisson-Voronoi tessellations in three-dimensional hyperbolic spaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 648-662
- Print publication:
- September 2000
-
- Article
- Export citation
Estimation of the intensity of stationary flat processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 114-139
- Print publication:
- March 2000
-
- Article
- Export citation
On the Steinhaus tiling problem
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-280
- Print publication:
- December 1999
-
- Article
- Export citation
A density bound for efficient packings of 3-space with centrally symmetric convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-144
- Print publication:
- June 1999
-
- Article
- Export citation
Isotropic surface area measures
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotic approximation of smooth convex bodies by general polytopes
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-125
- Print publication:
- June 1999
-
- Article
- Export citation
Kahane-Khinchine type inequalities for negative exponent
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 165-173
- Print publication:
- June 1999
-
- Article
- Export citation
Maximal hyperplane sections of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-136
- Print publication:
- June 1999
-
- Article
- Export citation
Random p-content of a p-parallelotope in Euclidean n-space
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 343-354
- Print publication:
- June 1999
-
- Article
- Export citation
Intersection bodies and polytopes
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 29-34
- Print publication:
- June 1999
-
- Article
- Export citation
Central limit theorem for a class of random measures associated with germ-grain models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 283-314
- Print publication:
- June 1999
-
- Article
- Export citation
Convex intersection bodies in three and four dimensions
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-27
- Print publication:
- June 1999
-
- Article
- Export citation
The convex hull of samples from self-similar distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 34-47
- Print publication:
- March 1999
-
- Article
- Export citation
Variance prediction under systematic sampling with geometric probes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 889-903
- Print publication:
- December 1998
-
- Article
- Export citation
Inequalities for dual isoperimetric deficits
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 269-285
- Print publication:
- December 1998
-
- Article
- Export citation
Minkowski sums of projections of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-268
- Print publication:
- December 1998
-
- Article
- Export citation