Refine listing
Actions for selected content:
326 results in 52Axx
Convex hulls of selected subsets of a Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 814-824
- Print publication:
- December 1992
-
- Article
- Export citation
On the mean value of the area of a random polygon in a plane convex body
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 279-290
- Print publication:
- December 1992
-
- Article
- Export citation
On the Busemann-Petty problem about convex, centrally symmetric bodies in ℝn
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 258-266
- Print publication:
- December 1992
-
- Article
- Export citation
Estimating sizes of a convex body by successive diameters and widths
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-257
- Print publication:
- December 1992
-
- Article
- Export citation
Minimal pairs of convex bodies in two dimensions
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 267-273
- Print publication:
- December 1992
-
- Article
- Export citation
Contact and chord length distributions of the Poisson Voronoi tessellation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 467-471
- Print publication:
- June 1992
-
- Article
- Export citation
Random polytopes in smooth convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-92
- Print publication:
- June 1992
-
- Article
- Export citation
Continuous selection theorem, coincidence theorem and intersection theorems concerning sets with H-convex sections
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-25
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
Conjugate points on convex surfaces
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 312-317
- Print publication:
- December 1991
-
- Article
- Export citation
The problem of illumination of the boundary of a convex body by affine subspaces
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 362-375
- Print publication:
- December 1991
-
- Article
- Export citation
Centrally symmetric convex bodies and Radon transforms on higher order Grassmannians
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-133
- Print publication:
- June 1991
-
- Article
- Export citation
On the union of convex bodies with no interior point in common
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-250
- Print publication:
- December 1990
-
- Article
- Export citation
A note on a problem of H. Busemann and C. M. Petty concerning sections of symmetric convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-244
- Print publication:
- December 1990
-
- Article
- Export citation
Minkowski surface area under affine transformations
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 232-238
- Print publication:
- December 1990
-
- Article
- Export citation
Surfaces with congruent shadow-lines
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-58
- Print publication:
- June 1990
-
- Article
- Export citation
On Eggleston's theorem about affine diameters
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-84
- Print publication:
- June 1990
-
- Article
- Export citation
On the product of distances to a point set on a sphere
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 466-482
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
Shadow boundaries of typical convex bodies. measure properties
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-152
- Print publication:
- June 1989
-
- Article
- Export citation
Stability in the Aleksandrov-Fenchel-Jessen Theorem
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-59
- Print publication:
- June 1989
-
- Article
- Export citation
Illuminating sets of constant width
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 180-189
- Print publication:
- December 1988
-
- Article
- Export citation
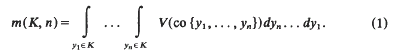
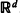 . Expressions are given for the spherical and linear contact distribution functions. These formulae lead to numerically tractable double-integral formulae for chord length probability density functions.
. Expressions are given for the spherical and linear contact distribution functions. These formulae lead to numerically tractable double-integral formulae for chord length probability density functions.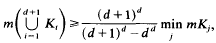
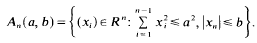
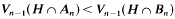 for every (
for every (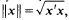 , and
, and 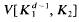 for the mixed volume
for the mixed volume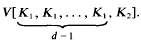
 and, for the variable point
and, for the variable point  from
from 