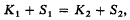Refine listing
Actions for selected content:
326 results in 52Axx
Inner contact measures
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-112
- Print publication:
- June 1979
-
- Article
- Export citation
Ellipsoids defined by Banach ideal norms
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-29
- Print publication:
- June 1979
-
- Article
- Export citation
An isoperimetric problem with lattice point constraints
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 1 / February 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-36
- Print publication:
- February 1979
-
- Article
-
- You have access
- Export citation
Isometries of the space of convex bodies of Ed
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 2 / December 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 270-278
- Print publication:
- December 1978
-
- Article
- Export citation
Sets homothetic to intersections of their translates
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 2 / December 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 264-269
- Print publication:
- December 1978
-
- Article
- Export citation
On three sets with no point in common
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-23
- Print publication:
- June 1978
-
- Article
- Export citation
A support characterization of zonotopes
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-16
- Print publication:
- June 1978
-
- Article
- Export citation
Kinematic measures for sets of colliding convex Bodies
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-12
- Print publication:
- June 1978
-
- Article
- Export citation
Centrally symmetric convex sets and mixed volumes
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-198
- Print publication:
- December 1977
-
- Article
- Export citation
Intersections of translates of convex sets
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-129
- Print publication:
- June 1977
-
- Article
- Export citation
Nonclosed simplices and quasi-simplices
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-85
- Print publication:
- June 1977
-
- Article
- Export citation
The existence of a centrally symmetric convex body with central sections that are unexpectedly small
- Part of
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 164-175
- Print publication:
- December 1975
-
- Article
- Export citation
A note on the false centre problem
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-227
- Print publication:
- December 1974
-
- Article
- Export citation
A decision procedure using the geometry of convex sets
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-206
- Print publication:
- December 1974
-
- Article
- Export citation
The convex generation of convex Borel sets in locally convex spaces
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-215
- Print publication:
- December 1974
-
- Article
- Export citation
Kinematic measures for sets of support figures
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 2 / December 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 270-281
- Print publication:
- December 1974
-
- Article
- Export citation
Shapes of worn stones
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-11
- Print publication:
- June 1974
-
- Article
- Export citation
Decomposition of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 19-25
- Print publication:
- June 1974
-
- Article
- Export citation
Problems related to a conjecture by Grünbaum
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-54
- Print publication:
- June 1974
-
- Article
- Export citation
On asymmetry classes of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 12-18
- Print publication:
- June 1974
-
- Article
- Export citation
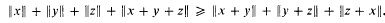
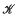 denote the class of all compact convex sets in Euclidean
denote the class of all compact convex sets in Euclidean  is non-empty for all families (
is non-empty for all families (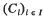 to have the intersection property.
to have the intersection property.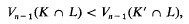
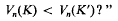
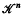 denote the set of all convex bodies in
denote the set of all convex bodies in