Refine listing
Actions for selected content:
326 results in 52Axx
Stability estimates for star bodies in terms of their intersection bodies
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 287-303
- Print publication:
- December 1998
-
- Article
- Export citation
The slices of a cone and a characterization of ellipsoids
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-317
- Print publication:
- December 1998
-
- Article
- Export citation
Inequalities for mixed stationary Poisson hyperplane tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 921-928
- Print publication:
- December 1998
-
- Article
- Export citation
Random nested tetrahedra
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 619-627
- Print publication:
- September 1998
-
- Article
- Export citation
On a random variable related to a system of convex bodies in the Euclidean space E n
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 335-341
- Print publication:
- June 1998
-
- Article
- Export citation
On the Hausdorff distance between a convex set and an interior random convex hull
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 295-316
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Euler Characteristics and imbeddings of hyperbolic Coxeter groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-161
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
On the mean shape of particle processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 890-908
- Print publication:
- December 1997
-
- Article
- Export citation
Few points to generate a random polytope
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 325-331
- Print publication:
- December 1997
-
- Article
- Export citation
A Steiner type formula for convex functions
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 195-214
- Print publication:
- June 1997
-
- Article
- Export citation
Covering convex bodies by translates of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-218
- Print publication:
- June 1997
-
- Article
- Export citation
A note on summands of compact convex sets
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 286-294
- Print publication:
- December 1996
-
- Article
- Export citation
Isoperimetric problems for polytopes with a given number of vertices
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 237-254
- Print publication:
- December 1996
-
- Article
- Export citation
Some results about Minkowski addition and difference
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 265-273
- Print publication:
- December 1996
-
- Article
- Export citation
Volumes of projection bodies
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 255-264
- Print publication:
- December 1996
-
- Article
- Export citation
Simple valuations on convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-39
- Print publication:
- June 1996
-
- Article
- Export citation
Estimation of oriented direction distribution of a planar body
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 394-404
- Print publication:
- June 1996
-
- Article
- Export citation
The sectional Poisson Voronoi tessellation is not a Voronoi tessellation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 356-376
- Print publication:
- June 1996
-
- Article
- Export citation
Rates of convergence for random approximations of convex sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 384-393
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
The uniform Kadec-Klee property for the Lorentz spaces Lw,1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-17
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
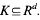 It is shown here that, with high probability,
It is shown here that, with high probability, 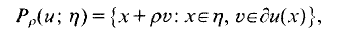
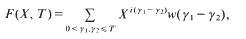
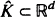 is studied. Basic inequalities are derived for the case of
is studied. Basic inequalities are derived for the case of 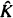 being a convex subset of
being a convex subset of 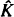 being the intersection of a random family of halfspaces containing
being the intersection of a random family of halfspaces containing 