Refine listing
Actions for selected content:
326 results in 52Axx
Foundations of a theory of convexity on affine Grassmann manifolds
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-328
- Print publication:
- December 1995
-
- Article
- Export citation
Invariance principle for the deviation between the probability content and the interior point proportion of a random convex hull
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1041-1047
- Print publication:
- December 1995
-
- Article
- Export citation
An elementary renewal theorem for random compact convex sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 931-942
- Print publication:
- December 1995
-
- Article
- Export citation
A short proof of Hadwiger's characterization theorem
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 329-339
- Print publication:
- December 1995
-
- Article
- Export citation
Intersection bodies and ellipsoids
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 295-304
- Print publication:
- December 1995
-
- Article
- Export citation
When can one domain enclose another in
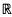 3?
3?
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 266-272
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Stereology for some classes of polyhedrons
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 384-396
- Print publication:
- June 1995
-
- Article
- Export citation
On second-order formulas in anisotropic stereology
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 326-343
- Print publication:
- June 1995
-
- Article
- Export citation
Two gradient properties of explicitly convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 404-410
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
How do convex bodies sit?
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-181
- Print publication:
- June 1995
-
- Article
- Export citation
On the volume of parallel bodies: a probabilistic derivation of the Steiner formula
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 97-101
- Print publication:
- March 1995
-
- Article
- Export citation
The Estimation of mean shape and mean particle number in overlapping particle systems in the plane
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 102-119
- Print publication:
- March 1995
-
- Article
- Export citation
Inequalities for the anisotropic Poisson polytope
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 56-62
- Print publication:
- March 1995
-
- Article
-
- You have access
- Export citation
On the approximation of a ball by random polytopes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 876-892
- Print publication:
- December 1994
-
- Article
- Export citation
The convex hull of a normal sample
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 855-875
- Print publication:
- December 1994
-
- Article
- Export citation
Hitting probabilities for random ellipses and ellipsoids
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 971-974
- Print publication:
- December 1993
-
- Article
- Export citation
Determination of convex bodies by their brightness functions
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-168
- Print publication:
- December 1993
-
- Article
- Export citation
The volume of the intersection of a convex body with its translates
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 278-289
- Print publication:
- December 1993
-
- Article
- Export citation
Orientation-dependent chord length distributions characterize convex polygons
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 730-736
- Print publication:
- September 1993
-
- Article
- Export citation
The convex hull of random balls
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 373-394
- Print publication:
- June 1993
-
- Article
- Export citation
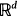 is investigated. We obtain, in particular, an explicit and distribution-independent bound.
is investigated. We obtain, in particular, an explicit and distribution-independent bound.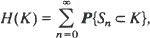
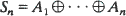 are Minkowski (element-wise) sums of i.i.d. random compact convex sets. In this paper we determine the limit of
are Minkowski (element-wise) sums of i.i.d. random compact convex sets. In this paper we determine the limit of 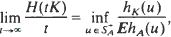
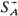 is the set of all unit vectors
is the set of all unit vectors 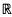
 be a sequence of independent and identically distributed random vectors drawn from the
be a sequence of independent and identically distributed random vectors drawn from the  2 we prove that the limiting distribution of Δ(
2 we prove that the limiting distribution of Δ( for
for 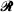 denote a rectangular lattice in the Euclidean plane
denote a rectangular lattice in the Euclidean plane 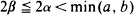 intersects
intersects  . We regard the lattice
. We regard the lattice  as the union of two orthogonal sets
as the union of two orthogonal sets  and
and 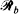 of equidistant lines and evaluate the probability that the random ellipse intersects
of equidistant lines and evaluate the probability that the random ellipse intersects 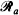 or
or 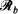 . Moreover, we consider the dependence structure of the events that the ellipse intersects
. Moreover, we consider the dependence structure of the events that the ellipse intersects 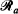 or
or 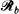 . We study further the case when the main axes of the ellipse are parallel to the lines of the lattice and satisfy 2
. We study further the case when the main axes of the ellipse are parallel to the lines of the lattice and satisfy 2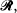 within the ellipse. We evaluate the distribution function, density, mean and variance of the length of these segments. We conclude with a generalization of this problem in three dimensions.
within the ellipse. We evaluate the distribution function, density, mean and variance of the length of these segments. We conclude with a generalization of this problem in three dimensions.