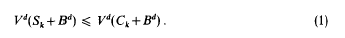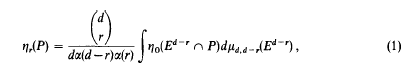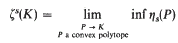Refine listing
Actions for selected content:
326 results in 52Axx
Convex bodies, economic cap coverings, random polytopes
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 274-291
- Print publication:
- December 1988
-
- Article
- Export citation
A geometric property of convex sets with applications to minimax type inequalities and fixed point theorems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-183
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
A maximally symmetric polyhedron of genus 3 with 10 vertices
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 237-242
- Print publication:
- December 1987
-
- Article
- Export citation
Maximally symmetric polyhedral realizations of Dyck's regular map
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-236
- Print publication:
- December 1987
-
- Article
- Export citation
Typical Convex Sets of Convex Sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-290
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
On the measure of the one-skeleton of the sum of convex compact sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-389
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
On extremal points of the unit ball in the Banach space of Lipschitz continuous functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 95-98
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
The number of polytopes, configurations and real matroids
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-71
- Print publication:
- June 1986
-
- Article
- Export citation
Convex bodies equidecomposable by locally discrete groups of isometries
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1985
-
- Article
- Export citation
Centrally symmetric convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-322
- Print publication:
- December 1984
-
- Article
- Export citation
The Hausdorff distance between compact convex sets
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-82
- Print publication:
- June 1984
-
- Article
- Export citation
A non-Schlegelian polyhedral map on the torus
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-88
- Print publication:
- June 1984
-
- Article
- Export citation
Connectivity and freely rolling convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 249-259
- Print publication:
- December 1982
-
- Article
- Export citation
Slices of L. Fejes Tóth's sausage conjecture
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 194-201
- Print publication:
- December 1982
-
- Article
- Export citation
Intersections of tangent convex curves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 456-458
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
On simplices and lattice points
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-19
- Print publication:
- June 1981
-
- Article
-
- You have access
- Export citation
Semiconvex geometry
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 496-510
- Print publication:
- April 1981
-
- Article
-
- You have access
- Export citation
Skeleta and sections of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 27 / Issue 1 / June 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-103
- Print publication:
- June 1980
-
- Article
- Export citation
The d – 2 Skeletons of polytopal approximations to a convex body in Ed
- Part of
-
- Journal:
- Mathematika / Volume 27 / Issue 1 / June 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-133
- Print publication:
- June 1980
-
- Article
- Export citation
Symmetrization and currents
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 269-289
- Print publication:
- December 1979
-
- Article
- Export citation
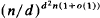 , as
, as 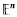 with mean width equal to that of a line segment of length 2 and with Steiner point at the origin is contained in the unit ball. As a consequence, the diameter with respect to the Hausdorff metric of the space of all such sets is 1. There also results a sharp bound for the Hausdorff distance between any two compact convex sets.
with mean width equal to that of a line segment of length 2 and with Steiner point at the origin is contained in the unit ball. As a consequence, the diameter with respect to the Hausdorff metric of the space of all such sets is 1. There also results a sharp bound for the Hausdorff distance between any two compact convex sets.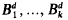 be
be