Refine listing
Actions for selected content:
326 results in 52Axx
NEW RESULTS FOR T(k)-FAMILIES IN THE PLANE
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 86-92
- Print publication:
- January 2010
-
- Article
- Export citation
THE AVERAGE DISTANCE BETWEEN TWO POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 October 2009, pp. 353-359
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
The chord length distribution function for regular polygons
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 358-366
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
DUALITY FOR CONVEX POLYTOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 399-412
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Random Laguerre tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 630-650
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
ARITHMETIC MEAN OF VALUES AND VALUE AT MEAN OF ARGUMENTS FOR CONVEX FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 137-141
-
- Article
-
- You have access
- Export citation
Estimation of the mean normal measure from flat sections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 31-48
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
On weak stationarity and weak isotropy of processes of convex bodies and cylinders
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 864-882
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
The Upper-Bound Theorem for Families of Boxes in ℝd
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 25-34
- Print publication:
- December 2007
-
- Article
- Export citation
Rotation Invariant Minkowski Classes of Convex Bodies
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 1-13
- Print publication:
- December 2007
-
- Article
- Export citation
Variations of Classic Characterizations of Ellipsoids and a Short Proof of the False Centre Theorem
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 35-40
- Print publication:
- December 2007
-
- Article
- Export citation
Shaken False Centre Theorem, I
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 41-46
- Print publication:
- December 2007
-
- Article
- Export citation
Nakajima's Problem: Convex Bodies of Constant Width and Constant Brightness
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 15-24
- Print publication:
- December 2007
-
- Article
- Export citation
Retrieving convex bodies from restricted covariogram functions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 613-629
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
A generalization of the matrix form of the Brunn-Minkowski inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-134
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Intersection densities of nonstationary Poisson processes of hypersurfaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 307-317
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
A connection between the volume fractions of the Stienen model and the dead leaves model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 41-52
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
A Large Deviations Approach to the Geometry of Random Polytopes
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 2 / December 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 173-210
- Print publication:
- December 2006
-
- Article
- Export citation
The Exact Distribution of the Number of Vertices of a Random Convex Chain
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 2 / December 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 247-254
- Print publication:
- December 2006
-
- Article
- Export citation
The Lower Dimensional Busemann-Petty Problem with Weights
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 2 / December 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 235-245
- Print publication:
- December 2006
-
- Article
- Export citation
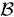 be a family of axis-aligned parallelotopes, or boxes, in ℝ
be a family of axis-aligned parallelotopes, or boxes, in ℝ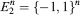 . Understanding the complexity of this class of polytopes is important for the “polyhedral combinatorics” approach to combinatorial optimization, and was put forward by Ziegler in [
. Understanding the complexity of this class of polytopes is important for the “polyhedral combinatorics” approach to combinatorial optimization, and was put forward by Ziegler in [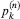 be the probability that the convex chain consists – apart from the points (0, 1) and (1, 0) – of exactly
be the probability that the convex chain consists – apart from the points (0, 1) and (1, 0) – of exactly 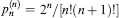 . The values of
. The values of 