Refine listing
Actions for selected content:
326 results in 52Axx
HYPERPLANES OF FINITE-DIMENSIONAL NORMED SPACES WITH THE MAXIMAL RELATIVE PROJECTION CONSTANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 02 March 2015, pp. 447-463
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
SEPARATION OF CONVEX SETS IN EXTENDED NORMED SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 145-165
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
EXTREMAL PERIMETERS OF QUADRANGLES IN THE PONCELET PORISM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 13 February 2015, pp. 487-501
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
CONCAVITY PROPERTIES OF EXTENSIONS OF THE PARALLEL VOLUME
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 13 January 2015, pp. 266-282
- Print publication:
- 2016
-
- Article
- Export citation
SUCCESSIVE RADII OF FAMILIES OF CONVEX BODIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 15 December 2014, pp. 331-344
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF 1-SEPARATED SEQUENCES ON THE UNIT BALL OF A FINITE-DIMENSIONAL BANACH SPACE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 547-558
- Print publication:
- September 2015
-
- Article
- Export citation
SHARPENING GEOMETRIC INEQUALITIES USING COMPUTABLE SYMMETRY MEASURES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 559-580
- Print publication:
- September 2015
-
- Article
- Export citation
Statistics for Poisson Models of Overlapping Spheres
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 937-962
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On Random Disc Polygons in Smooth Convex Discs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 899-918
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Size distributions in random triangles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 283-295
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On the Volume of the Zero Cell of a Class of Isotropic Poisson Hyperplane Tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 622-642
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Random Symmetrizations of Convex Bodies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 603-621
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
EXTENSIONS OF TRANSLATION INVARIANT VALUATIONS ON POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 19 August 2014, pp. 236-258
- Print publication:
- January 2015
-
- Article
- Export citation
INVERSE BERNSTEIN INEQUALITIES AND MIN–MAX–MIN PROBLEMS ON THE UNIT CIRCLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 581-590
- Print publication:
- September 2015
-
- Article
- Export citation
SUM THEOREMS FOR MAXIMALLY MONOTONE OPERATORS OF TYPE (FPV)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 1-26
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
CONVEX CURVES AND A POISSON IMITATION OF LATTICES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 139-152
- Print publication:
- January 2014
-
- Article
- Export citation
A NOTE ON ORDER-TYPE HOMOGENEOUS POINT SETS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 19 December 2013, pp. 37-42
- Print publication:
- January 2014
-
- Article
- Export citation
Exact Formulae for Variances of Functionals of Convex Hulls
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 917-924
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
INTERSECTIONS OF BALLS AND SETS OF CONSTANT WIDTH IN FINITE-DIMENSIONAL NORMED SPACES
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 28 March 2013, pp. 477-492
- Print publication:
- July 2013
-
- Article
- Export citation
Set Reconstruction by Voronoi Cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 938-953
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
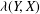
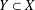
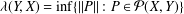
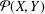
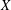
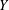

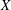
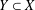
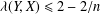
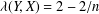
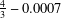
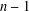
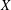

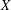
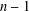
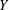
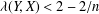
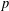
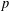
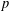
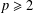
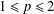
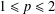
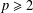
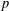
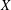
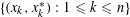
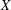
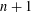
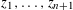
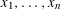
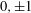
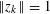
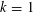
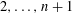
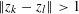
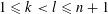
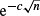 with
with 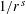
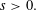
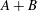
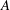
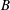
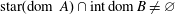
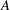
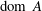
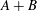
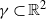
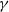


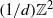
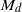
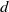
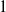
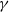
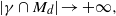
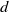
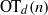
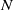
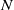
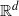

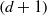
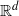
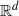
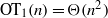
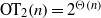
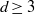
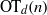
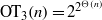
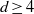
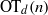
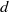
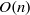
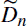 . These formulae are in line with asymptotic distribution results in Groeneboom (1988), Nagaev and Khamdamov (1991), and Groeneboom (2012), as well as with recent results in Pardon (2011), (2012).
. These formulae are in line with asymptotic distribution results in Groeneboom (1988), Nagaev and Khamdamov (1991), and Groeneboom (2012), as well as with recent results in Pardon (2011), (2012).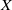
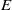
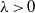
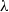
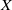
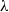
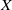
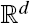 of intensity λ>0, define the Poisson–Voronoi approximation
of intensity λ>0, define the Poisson–Voronoi approximation 