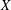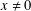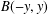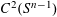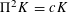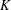Refine listing
Actions for selected content:
326 results in 52Axx
SPACES OF SPECIAL QUADRILATERALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 155-167
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ON THE INTEGRAL FORMULAS OF CROFTON AND HURWITZ RELATIVE TO THE VISUAL ANGLE OF A CONVEX SET
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 21 May 2019, pp. 874-896
- Print publication:
- 2019
-
- Article
- Export citation
ELLIPSOIDS ARE THE ONLY LOCAL MAXIMIZERS OF THE VOLUME PRODUCT
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 500-504
- Print publication:
- 2019
-
- Article
-
- You have access
- HTML
- Export citation
FLAG AREA MEASURES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 23 July 2019, pp. 958-989
- Print publication:
- 2019
-
- Article
- Export citation
POSITIVE CENTRE SETS OF CONVEX CURVES AND A BONNESEN TYPE INEQUALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 293-301
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A conditional limit theorem for high-dimensional ℓᵖ-spheres
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1060-1077
- Print publication:
- December 2018
-
- Article
- Export citation
Variance estimates for random disc-polygons in smooth convex discs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1143-1157
- Print publication:
- December 2018
-
- Article
- Export citation
Limit theorems for random polytopes with vertices on convex surfaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1227-1245
- Print publication:
- December 2018
-
- Article
- Export citation
THE ISOPERIMETRIC QUOTIENT OF A CONVEX BODY DECREASES MONOTONICALLY UNDER THE EIKONAL ABRASION MODEL
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 119-129
- Print publication:
- 2019
-
- Article
- Export citation
THE ROSENTHAL–SZASZ INEQUALITY FOR NORMED PLANES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 29 August 2018, pp. 130-136
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF EUCLIDEAN NORMED PLANES VIA BISECTORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 August 2018, pp. 121-129
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Reverse Faber–Krahn and Mahler inequalities for the Cheeger constant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 913-937
- Print publication:
- October 2018
-
- Article
- Export citation
DEFORMING A CONVEX DOMAIN INTO A DISK BY KLAIN’S CYCLIC REARRANGEMENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 313-319
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
A LOCAL UNIQUENESS THEOREM FOR MINIMIZERS OF PETTY’S CONJECTURED PROJECTION INEQUALITY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 24 January 2018, pp. 1-19
- Print publication:
- 2018
-
- Article
- Export citation
AN INCLUSION–EXCLUSION IDENTITY FOR NORMAL CONES OF POLYHEDRAL SETS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 05 February 2018, pp. 124-136
- Print publication:
- 2018
-
- Article
- Export citation
Octahedrality in Lipschitz-free Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 447-460
- Print publication:
- June 2018
-
- Article
- Export citation
Robust Tverberg and Colourful Carathéodory Results via Random Choice
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 19 December 2017, pp. 427-440
-
- Article
- Export citation
Convex Polygons in Geometric Triangulations†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 30 May 2017, pp. 641-659
-
- Article
- Export citation
A NOTE ON MARKOVIAN QUANTUM DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 436-445
-
- Article
-
- You have access
- Export citation
Total Variation Based Parameter-Free Model for Impulse Noise Removal
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 186-204
- Print publication:
- February 2017
-
- Article
- Export citation