Refine listing
Actions for selected content:
326 results in 52Axx
NON-UNIQUENESS OF CONVEX BODIES WITH PRESCRIBED VOLUMES OF SECTIONS AND PROJECTIONS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 01 August 2012, pp. 213-221
- Print publication:
- January 2013
-
- Article
- Export citation
NEIGHBORLINESS OF THE SYMMETRIC MOMENT CURVE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 April 2012, pp. 223-249
- Print publication:
- January 2013
-
- Article
- Export citation
ON THE EXISTENCE OF SUPERGAUSSIAN DIRECTIONS ON CONVEX BODIES
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 24 November 2011, pp. 389-408
- Print publication:
- July 2012
-
- Article
- Export citation
A large deviation principle for Minkowski sums of heavy-tailed random compact convex sets with finite expectation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue A / August 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 133-144
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ORBITOPES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 29 June 2011, pp. 275-314
- Print publication:
- July 2011
-
- Article
- Export citation
VOLUMES OF PROJECTION BODIES OF SOME CLASSES OF CONVEX BODIES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 329-353
- Print publication:
- July 2011
-
- Article
- Export citation
ON THE MONOTONICITY OF THE EXPECTED VOLUME OF A RANDOM SIMPLEX
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 20 June 2011, pp. 77-91
- Print publication:
- January 2012
-
- Article
- Export citation
Curves of infinite length in labyrinth fractals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 329-344
-
- Article
-
- You have access
- Export citation
DECOMPOSITION OF BALLS INTO CONGRUENT PIECES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 21 January 2011, pp. 89-107
- Print publication:
- January 2011
-
- Article
- Export citation
LOCAL MINIMALITY OF THE VOLUME-PRODUCT AT THE SIMPLEX
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 13 December 2010, pp. 121-134
- Print publication:
- January 2011
-
- Article
- Export citation
PARALLEL BODIES AND NORMALS OF CONVEX BODIES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 13 December 2010, pp. 109-119
- Print publication:
- January 2011
-
- Article
- Export citation
Intrinsic volumes of inscribed random polytopes in smooth convex bodies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 605-619
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
STABILITY OF THE PRÉKOPA–LEINDLER INEQUALITY
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 13 July 2010, pp. 339-356
- Print publication:
- July 2010
-
- Article
- Export citation
CHARACTERIZATION OF ELLIPSOIDS BY MEANS OF PARALLEL TRANSLATED SECTIONS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 13 July 2010, pp. 363-378
- Print publication:
- July 2010
-
- Article
- Export citation
COVARIOGRAM OF NON-CONVEX SETS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 21 June 2010, pp. 267-284
- Print publication:
- July 2010
-
- Article
- Export citation
ON THE MAXIMIZATION OF A CLASS OF FUNCTIONALS ON CONVEX REGIONS, AND THE CHARACTERIZATION OF THE FARTHEST CONVEX SET
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 18 May 2010, pp. 245-265
- Print publication:
- July 2010
-
- Article
- Export citation
TILINGS OF HILBERT SPACES
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 29 April 2010, pp. 217-230
- Print publication:
- July 2010
-
- Article
- Export citation
Contact and Chord Length Distribution Functions of the Poisson-Voronoi Tessellation in High Dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 48-68
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
ON EMBEDDINGS OF FINITE METRIC SPACES IN ln∞
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 135-139
- Print publication:
- January 2010
-
- Article
- Export citation
VARIATION ON A THEOREM BY CARATHÉODORY
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 169-172
- Print publication:
- January 2010
-
- Article
- Export citation
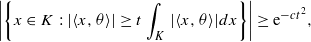
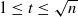 , where
, where 