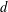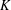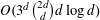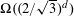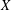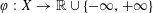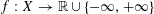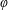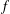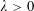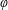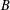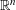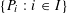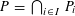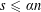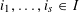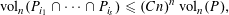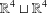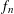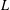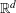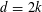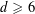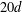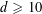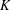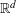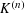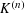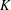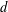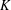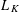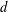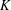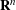Refine listing
Actions for selected content:
326 results in 52Axx
ARRANGEMENTS OF HOMOTHETS OF A CONVEX BODY
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 09 August 2017, pp. 696-710
- Print publication:
- 2017
-
- Article
- Export citation
ENVELOPES FOR SETS AND FUNCTIONS: REGULARIZATION AND GENERALIZED CONJUGACY
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 23 February 2017, pp. 383-432
- Print publication:
- 2017
-
- Article
- Export citation
ILLUMINATION OF CONVEX BODIES WITH MANY SYMMETRIES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 16 February 2017, pp. 372-382
- Print publication:
- 2017
-
- Article
- Export citation
BRASCAMP–LIEB INEQUALITY AND QUANTITATIVE VERSIONS OF HELLY’S THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 272-291
- Print publication:
- 2017
-
- Article
- Export citation
On long-range dependence of random measures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1235-1255
- Print publication:
- December 2016
-
- Article
- Export citation
COMPACTNESS OF SPACES OF CONVEX AND SIMPLE QUADRILATERALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 09 September 2016, pp. 507-521
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
A Two-Stage Image Segmentation Model for Multi-Channel Images
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 904-926
- Print publication:
- April 2016
-
- Article
- Export citation
A general formula for the anisotropic outer Minkowski content of a set
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 393-413
- Print publication:
- April 2016
-
- Article
- Export citation
DUALITY FOR QUASIPOLYTOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 95-117
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
THE GREEN–OSHER INEQUALITY IN RELATIVE GEOMETRY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 155-164
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Characterization of ellipsoids as K-dense sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 07 January 2016, pp. 213-223
- Print publication:
- February 2016
-
- Article
- Export citation
ON THE MONOTONICITY OF THE MOMENTS OF VOLUMES OF RANDOM SIMPLICES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 949-958
- Print publication:
- 2016
-
- Article
- Export citation
MORE ON LOGARITHMIC SUMS OF CONVEX BODIES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 10 May 2016, pp. 818-841
- Print publication:
- 2016
-
- Article
- Export citation
A GENERALIZATION OF THE DISCRETE VERSION OF MINKOWSKI’S FUNDAMENTAL THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 29 February 2016, pp. 637-652
- Print publication:
- 2016
-
- Article
- Export citation
A SPIKY BALL
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 630-636
- Print publication:
- 2016
-
- Article
- Export citation
DECOMPOSITION OF BALLS IN
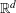 $\mathbb{R}^{d}$
$\mathbb{R}^{d}$
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 378-405
- Print publication:
- 2016
-
- Article
- Export citation
TWO OPTIMISATION PROBLEMS FOR CONVEX BODIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 05 August 2015, pp. 137-145
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
THE VOLUME OF RANDOM POLYTOPES CIRCUMSCRIBED AROUND A CONVEX BODY
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 June 2015, pp. 283-306
- Print publication:
- 2016
-
- Article
- Export citation
A SIMPLICIAL POLYTOPE THAT MAXIMIZES THE ISOTROPIC CONSTANT MUST BE A SIMPLEX
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 May 2015, pp. 307-320
- Print publication:
- 2016
-
- Article
- Export citation
ESTIMATES FOR SOLUTIONS TO DISCRETE CONVOLUTION EQUATIONS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 15 April 2015, pp. 295-308
- Print publication:
- May 2015
-
- Article
- Export citation