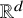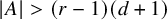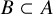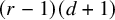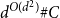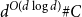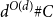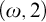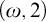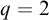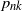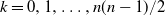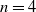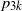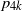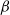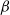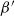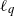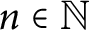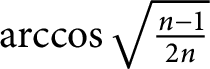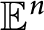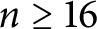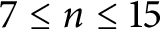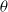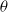Refine listing
Actions for selected content:
326 results in 52Axx
Series expansions for random disc-polygons in smooth plane convex bodies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1407-1423
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extensions of the colorful Helly theorem for d-collapsible and d-Leray complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds for a discrete John’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 484-486
-
- Article
- Export citation
On the cross-product conjecture for the number of linear extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 535-562
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Affine isoperimetric inequalities on flag manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 19 December 2023, pp. 252-281
- Print publication:
- February 2025
-
- Article
- Export citation
Convexity of the radial sum of a star body and a ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 289-303
- Print publication:
- June 2024
-
- Article
- Export citation
A minimax inequality for inscribed cones revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 31 August 2023, pp. 215-221
- Print publication:
- March 2024
-
- Article
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEFINABLE
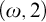 $(\omega ,2)$-THEOREM FOR FAMILIES WITH VC-CODENSITY LESS THAN
$(\omega ,2)$-THEOREM FOR FAMILIES WITH VC-CODENSITY LESS THAN 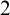 $2$
$2$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1659-1668
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting shape for first-passage percolation models on random geometric graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1367-1385
- Print publication:
- December 2023
-
- Article
- Export citation
Magnitude and Holmes–Thompson intrinsic volumes of convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 854-867
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Curvature functionals on convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 761-779
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On intersection probabilities of four lines inside a planar convex domain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 December 2022, pp. 504-527
- Print publication:
- June 2023
-
- Article
- Export citation
Reconstruction problems of convex bodies from surface area measures and lightness functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1685-1710
- Print publication:
- October 2023
-
- Article
- Export citation
Crofton formulas in pseudo-Riemannian space forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 28 October 2022, pp. 1935-1979
- Print publication:
- October 2022
-
- Article
- Export citation
The
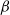 $\beta$-Delaunay tessellation: Description of the model and geometry of typical cells
$\beta$-Delaunay tessellation: Description of the model and geometry of typical cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 01 August 2022, pp. 1252-1290
- Print publication:
- December 2022
-
- Article
- Export citation
Limit theorems for random points in a simplex
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 June 2022, pp. 685-701
- Print publication:
- September 2022
-
- Article
- Export citation
On the roots of polynomials with log-convex coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 470-493
- Print publication:
- April 2023
-
- Article
- Export citation
Spherical coverings and X-raying convex bodies of constant width
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 860-866
- Print publication:
- December 2022
-
- Article
- Export citation
On point processes defined by angular conditions on Delaunay neighbors in the Poisson–Voronoi Tessellation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 952-965
- Print publication:
- December 2021
-
- Article
- Export citation