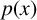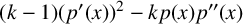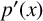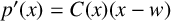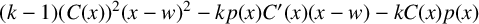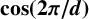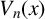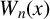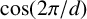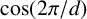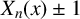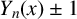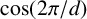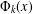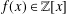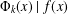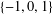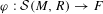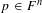Refine listing
Actions for selected content:
13 results in 12Dxx
UPPER BOUNDS ON POLYNOMIAL ROOT SEPARATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 274-289
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometry of tropical extensions of hyperfields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positive Ulrich sheaves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 April 2023, pp. 881-914
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NUMBER OF REAL ZEROS OF POLYNOMIALS OF EVEN DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 89-93
- Print publication:
- February 2024
-
- Article
- Export citation
Polynomials over structured grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 284-298
-
- Article
- Export citation
FACTORING VARIANTS OF CHEBYSHEV POLYNOMIALS WITH MINIMAL POLYNOMIALS OF
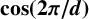 $\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
$\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 448-457
- Print publication:
- December 2022
-
- Article
- Export citation
STRICTLY REAL FUNDAMENTAL THEOREM OF ALGEBRA USING POLYNOMIAL INTERLACING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 249-255
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
CYCLOTOMIC FACTORS OF BORWEIN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 41-47
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
CONTINUITY OF ROOTS, REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 448-455
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Bounding the Number of Common Zeros of Multivariate Polynomials and Their Consecutive Derivatives
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 03 August 2018, pp. 253-279
-
- Article
- Export citation
ON THE SUBSTITUTION THEOREM FOR RINGS OF SEMIALGEBRAIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 01 July 2014, pp. 857-894
- Print publication:
- October 2015
-
- Article
- Export citation
ON THE EQUATION f(g(x))=f(x)hm(x) FOR COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 155-161
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Bounds for the multiplicities of the roots of a complex polynomial
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 08 April 2011, pp. 587-598
-
- Article
-
- You have access
- Export citation