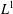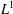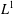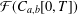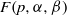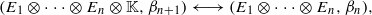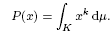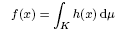Refine listing
Actions for selected content:
57 results in 46Gxx
The Spectra of Algebras of Group-Symmetric Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 609-623
-
- Article
- Export citation
THE BOUNDED APPROXIMATION PROPERTY FOR THE WEIGHTED SPACES OF HOLOMORPHIC MAPPINGS ON BANACH SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 07 September 2017, pp. 307-320
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
The algebra of symmetric analytic functions on L ∞
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 743-761
- Print publication:
- August 2017
-
- Article
- Export citation
Corrigendum and Addendum: Abstract M- and Abstract L-Spaces of Polynomials on Banach Lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 877-879
-
- Article
- Export citation
FACTORIZATION OF OPERATORS THROUGH SUBSPACES OF
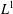 $L^{1}$ -SPACES
$L^{1}$ -SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 313-328
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Coincidence Results for Summing Multilinear Mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 03 June 2016, pp. 877-897
-
- Article
- Export citation
A TRANSLATION THEOREM FOR THE GENERALISED ANALYTIC FEYNMAN INTEGRAL ASSOCIATED WITH GAUSSIAN PATHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 09 September 2015, pp. 152-161
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
SOME COMMENTS ON SCALAR DIFFERENTIATION OF VECTOR-VALUED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 311-321
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
HOLOMORPHIC SUPERPOSITION OPERATORS BETWEEN BANACH FUNCTION SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 186-197
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ON PERIODIC SOLUTIONS FOR FIRST-ORDER DIFFERENTIAL EQUATIONS INVOLVING THE DISTRIBUTIONAL HENSTOCK–KURZWEIL INTEGRAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 06 February 2012, pp. 327-338
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
The Darboux problem involving the distributional Henstock–Kurzweil integral
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 04 January 2012, pp. 197-205
-
- Article
-
- You have access
- Export citation
Some algebras of symmetric analytic functions and their spectra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 20 June 2011, pp. 125-142
-
- Article
-
- You have access
- Export citation
POINTWISE CONVERGENCE AND SEMIGROUPS ACTING ON VECTOR-VALUED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 22 March 2011, pp. 44-48
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON THE REPRESENTATION OF MULTI-IDEALS BY TENSOR NORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 09 February 2011, pp. 253-269
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
INTERSECTIONS OF HOLOMORPHIC RETRACTS IN BANACH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 04 January 2011, pp. 297-307
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Orthogonally additive holomorphic functions of bounded type over C(K)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 609-618
-
- Article
-
- You have access
- Export citation
TENSOR PRODUCT REPRESENTATION OF THE (PRE)DUAL OF THE Lp-SPACE OF A VECTOR MEASURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 211-225
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
A CHARACTERIZATION OF THE WEAK RADON–NIKODÝM PROPERTY BY FINITELY ADDITIVE INTERVAL FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 07 September 2009, pp. 476-485
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
SOME EXAMPLES IN VECTOR INTEGRATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 384-392
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
p-VARIATION OF VECTOR MEASURES WITH RESPECT TO BILINEAR MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 411-430
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
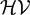
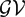
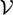
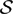
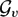
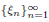 such that
such that 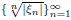 is bounded and turns to be separable. All this follows from our main result that the subalgebra of
is bounded and turns to be separable. All this follows from our main result that the subalgebra of