Refine listing
Actions for selected content:
57 results in 46Gxx
Spaces of vector functions that are integrable with respect to vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-109
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
On symmetric ideals of multilinear mappings between Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-148
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
The multidirectional mean value inequalities with second order information
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-172
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Nuclear and integral polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-280
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Bilinear integration with positive vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-294
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Unique Hahn-Banach theorems for spaces of homogeneous polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 387-400
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
The bounded vector measure associated to a conical measure and pettis differentiability
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 10-36
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
A Radon-Nikodým theorem for vector polymeasures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-200
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation
Operators and the space of integrable scalar functions with respect to a Fréchet-valued measure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 176-193
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
The second dual of C0 (S, A)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-313
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Integral representation theorems in partially ordered vector spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-215
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
On transition multimeasures with values in a Banach space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 72-89
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Archimedes integrals and conuclear spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 22-31
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Scalar operators and integration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 3 / December 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-420
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
A concrete realization of the dual space of L1-spaces of certain vector and operator-valued measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 265-279
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Approximate subdifferentials and applications II
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-128
- Print publication:
- June 1986
-
- Article
- Export citation
Multipliers of Banach valued function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-62
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
 (
(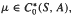 ,
,