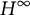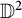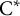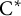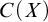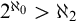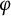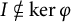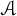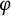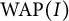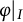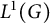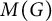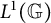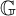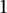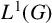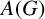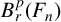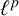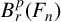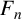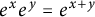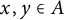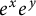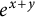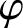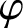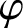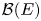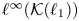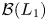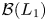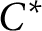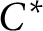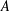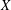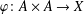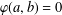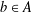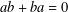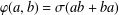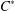Refine listing
Actions for selected content:
97 results in 46Hxx
Continuity and realization of multiplicative maps between RKHS and their cyclicity preserving properties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-14
-
- Article
- Export citation
MULTIPLICATIVE (IN)STABILITY OF BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 194-200
- Print publication:
- August 2025
-
- Article
- Export citation
MORE ON RESTRICTED BOUNDARIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 334-344
- Print publication:
- October 2025
-
- Article
- Export citation
Fredholm index of Toeplitz pairs with
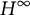 $H^{\infty }$ symbols
$H^{\infty }$ symbols
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 10 December 2024, pp. 166-176
- Print publication:
- March 2025
-
- Article
- Export citation
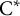 $\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
$\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 November 2024, pp. 1081-1091
- Print publication:
- December 2024
-
- Article
- Export citation
Weak amenability for dual Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 740-748
-
- Article
- Export citation
DISCONTINUOUS HOMOMORPHISMS OF
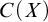 $C(X)$ WITH
$C(X)$ WITH 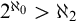 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 665-696
- Print publication:
- June 2024
-
- Article
- Export citation
A COUNTEREXAMPLE TO A RESULT OF JABERI AND MAHMOODI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 10 August 2023, pp. 155-157
- Print publication:
- August 2024
-
- Article
- Export citation
On the Dales–Żelazko conjecture for Beurling algebras on discrete groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 613-624
-
- Article
- Export citation
THE RESTRICTED CONNECTED HULL: FILLING THE HOLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 April 2023, pp. 388-392
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable finiteness does not imply linear soficity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 319-325
- Print publication:
- September 2023
-
- Article
- Export citation
Invariant means on weakly almost periodic functionals with application to quantum groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 927-936
- Print publication:
- September 2023
-
- Article
- Export citation
MULTIPLIERS ON THE SECOND DUAL OF ABSTRACT SEGAL ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 133-141
- Print publication:
- August 2023
-
- Article
- Export citation
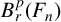 $B^p_r(F_n)$ HAS NO NONTRIVIAL IDEMPOTENTS
$B^p_r(F_n)$ HAS NO NONTRIVIAL IDEMPOTENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 142-149
- Print publication:
- August 2023
-
- Article
- Export citation
Commutativity via spectra of exponentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 815-824
- Print publication:
- December 2022
-
- Article
- Export citation
ON
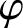 $\varphi $-AMENABILITY OF DUAL BANACH ALGEBRAS
$\varphi $-AMENABILITY OF DUAL BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 09 July 2021, pp. 303-313
- Print publication:
- April 2022
-
- Article
- Export citation
A short proof that ℬ(L1) is not amenable
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 1758-1767
- Print publication:
- December 2021
-
- Article
- Export citation
Ring-theoretic (In)finiteness in reduced products of Banach algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1423-1458
- Print publication:
- October 2021
-
- Article
- Export citation
Ideals of the Quantum Group Algebra, Arens Regularity and Weakly Compact Multipliers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 825-836
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
ZERO JORDAN PRODUCT DETERMINED BANACH ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 145-158
-
- Article
- Export citation