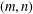 $(m,n)$-JORDAN DERIVATIONS OF RINGS AND BANACH ALGEBRAS
$(m,n)$-JORDAN DERIVATIONS OF RINGS AND BANACH ALGEBRAS
 $^{\ast }$-ALGEBRAS
$^{\ast }$-ALGEBRAS
 $\ast $-SEMISIMPLICITY OF THE
$\ast $-SEMISIMPLICITY OF THE 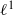 ${\ell }^{1} $-ALGEBRA ON AN ABELIAN
${\ell }^{1} $-ALGEBRA ON AN ABELIAN  $\ast $-SEMIGROUP
$\ast $-SEMIGROUP