Let $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H(\mathbb{D})$ denote the space of holomorphic functions on the unit disc $\mathbb{D}$. Given $p>0$ and a weight $\omega $, the Hardy growth space $H(p, \omega )$ consists of those $f\in H(\mathbb{D})$ for which the integral means $M_p(f,r)$ are estimated by $C\omega (r)$, $0<r<1$. Assuming that $p>1$ and $\omega $ satisfies a doubling condition, we characterise $H(p, \omega )$ in terms of associated Fourier blocks. As an application, extending a result by Bennett et al. [‘Coefficients of Bloch and Lipschitz functions’, Illinois J. Math. 25 (1981), 520–531], we compute the solid hull of $H(p, \omega )$ for $p\ge 2$.

In this paper, we investigate the properties of locally univalent and multivalent planar harmonic mappings. First, we discuss coefficient estimates and Landau’s theorem for some classes of locally univalent harmonic mappings, and then we study some Lipschitz-type spaces for locally univalent and multivalent harmonic mappings.

We first study the bounded mean oscillation of planar harmonic mappings. Then we establish a relationship between Lipschitz-type spaces and equivalent modulus of real harmonic mappings. Finally, we obtain sharp estimates on the Lipschitz number of planar harmonic mappings in terms of the bounded mean oscillation norm, which shows that the harmonic Bloch space is isomorphic to $BM{O}_{2} $ as a Banach space.

Carleson's corona theorem is used to obtain two results on cyclicity of singular inner functions in weighted Bergman-type spaces on the unit disk. Our method of proof requires no regularity conditions on the weights.

Let H1/2 be the Hardy space on the open unit disc. For two non-zero functions f and g in H1/2, we study the relation between f and g when f/g ≥ 0 a.e. on ∂D. Then we generalize a theorem of Neuwirth and Newman and Helson and Sarason with a simple proof.

In general, multiplication of operators is not essentially commutative in an algebra generated by integral-type operators and composition operators. In this paper, we characterize the essential commutativity of the integral operators and composition operators from a mixed-norm space to a Bloch-type space, and give a complete description of the universal set of integral operators. Corresponding results for boundedness and compactness are also obtained.

Let m be a measure supported on a relatively closed subset X of the unit disc. If f is a bounded function on the unit circle, let fm denote the restriction to X of the harmonic extension of f to the unit disc. We characterize those m such that the pre-adjoint of the linear map f → fm has a non-trivial kernel.

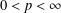
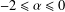
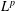
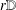
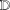
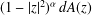
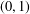
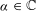
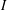
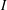
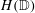
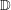
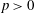
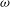
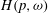
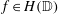
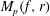
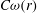
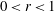
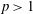
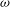
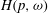
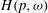
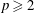
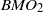
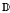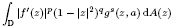
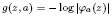An analytic function f in the unit disc belongs to F(p,q,s), if

is uniformly bounded for all a ∈ . Here is the Green function of 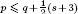, and φa(z)=(a−z)/(1−āz). It is shown that for 0 < γ < ∞ and |w|=1 the singular inner function exp(γ(z+w)/(z−w)) belongs to F(p,q,s), 0<s≤1, if and only if . Moreover, it is proved that, if 0<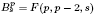s<1, then an inner function belongs to the Möbius invariant Besov-type space for some (equivalently for all) p > max{s,1−s} if and only if it is a Blaschke product whose zero sequence {zn} satisfies .

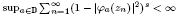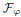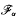
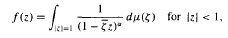In a scale of Fock spaces with radial weights ϕ we study the existence of Riesz bases of (normalized) reproducing kernels. We prove that these spaces possess such bases if and only if ϕ(x) grows at most like (log x)2.

We give two charaterizations of the Möbius invariant QK spaces, one in terms of a double integral and the other in terms of the mean oscillation in the Bergman metric. Both charaterizations avoid the use of derivatives. Our results are new even in the case of Qp.

For α > 0 let α denote the set of functions which can be expressed where μ is a complex-valued Borel measure on the unit circle. We show that if 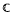f is an analytic function in Δ = {z ∈ : |z| < 1} and there are two nonparallel rays in /f(Δ) which do not meet, then f ∈ α where απ denotes the largest of the two angles determined by the rays. Also if the range of a function analytic in Δ is contained in an angular wedge of opening απ and 1 < α < 2, then f ∈ α.

This paper studies the concept of strongly omnipresent operators that was recently introduced by the first two authors. An operator T on the space H(G) of holomorphic functions on a complex domain G is called strongly omnipresent whenever the set of T-monsters is residual in H(G), and a T-monster is a function f such that Tf exhibits an extremely ‘wild’ behaviour near the boundary. We obtain sufficient conditions under which an operator is strongly omnipresent, in particular, we show that every onto linear operator is strongly omnipresent. Using these criteria we completely characterize strongly omnipresent composition and multiplication operators.

Hilbert spaces of analytic functions generated by rotationally symmetric measures on disks and annuli are studied. A domination relation between function norm and weighted sums of integral means on circles is developed. The function norm and the weighted sum take the same value for a specified class of polynomials. This class can be varied according to two parameters. Parts of the construction carry over to other Banach spaces of analytic of harmonic functions. Counterexamples illuminating properties of the complex method of interpolation appear as a byproduct.

Let W+ denote the Banach algebra of all absolutely convergent Taylor series in the open unit disc. We characterize the finitely generated closed and prime ideals in W+. Finally, we solve a problem of Rubel and McVoy by showing that W+ is not coherent.