Refine listing
Actions for selected content:
76 results in 08Axx
Congruence intersection properties for varieties of algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 104-121
-
- Article
-
- You have access
- Export citation
On five well-known commutator identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-19
-
- Article
-
- You have access
- Export citation
Simple surjective algebras having no proper subalgebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 434-454
-
- Article
-
- You have access
- Export citation
A Characterization of semiprime ideals in near-rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 2 / April 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-214
-
- Article
-
- You have access
- Export citation
On commutator laws in groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 95-103
-
- Article
-
- You have access
- Export citation
Strong and full dualisability: three-element unary algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-220
-
- Article
-
- You have access
- Export citation
Radical decompositions of idempotent algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 2 / April 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-236
-
- Article
-
- You have access
- Export citation
Endoprimal abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 3 / December 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 412-428
-
- Article
-
- You have access
- Export citation
Universal varieties of semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 2 / April 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-152
-
- Article
-
- You have access
- Export citation
Relatively free algebras with weak exchange properties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 355-384
-
- Article
-
- You have access
- Export citation
Uniform labelled semilattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-397
-
- Article
-
- You have access
- Export citation
Multialgebras, universal algebras and identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 121-140
-
- Article
-
- You have access
- Export citation
Strong duality for metacyclic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-392
-
- Article
-
- You have access
- Export citation
The subdirect decomposition theorem for classes of structures closed under direct limits
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-179
-
- Article
-
- You have access
- Export citation
Modular inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-63
-
- Article
-
- You have access
- Export citation
Medial idempotent groupoids III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 312-320
-
- Article
-
- You have access
- Export citation
Locally finite affine complete varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-159
-
- Article
-
- You have access
- Export citation
Fregean subtractive varieties with definable congruence
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 353-366
-
- Article
-
- You have access
- Export citation
Inverse semigroups determined by their lattices of inverse subsemigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 321-346
-
- Article
-
- You have access
- Export citation
Radicals and subdirect decompositions of Ω-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-198
-
- Article
-
- You have access
- Export citation
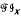 is determined by its lattice
is determined by its lattice 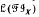 of inverse subsemigroups, in the sense that for any inverse semigroup
of inverse subsemigroups, in the sense that for any inverse semigroup 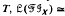
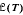 implies
implies 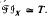 . (In fact, the lattice isomorphism is induced by an isomorphism of
. (In fact, the lattice isomorphism is induced by an isomorphism of 