Refine listing
Actions for selected content:
95 results in 54Cxx
Continuous nilpotents on topological spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 127-136
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Generalizations of F. E. Browder's sharpened form of the schauder fixed point theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 390-398
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
A Riemann integral in a locally compact Hausdorff space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 115-137
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
Semicontinuity of multifunctions connected with optimization with respect to cones
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-193
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Piece-wise closed functions and almost discretely σ-decomposable families
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-247
- Print publication:
- December 1985
-
- Article
- Export citation
One-point extensions of locally para-H-closed spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-142
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
On semi-regularization topologies
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 40-54
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
Invariance of infinite-dimensional classes of spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 76-83
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
Compactness of subsets of Tychonoff sets via exponential laws
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 3 / June 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 368-376
- Print publication:
- June 1983
-
- Article
-
- You have access
- Export citation
On almost locally connected spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-264
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation
A note on pseudocompact spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 4 / June 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 408-410
- Print publication:
- June 1979
-
- Article
-
- You have access
- Export citation
Characterization of pseudocompactness by the topology of uniform convergence on function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 26 / Issue 2 / September 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-256
- Print publication:
- September 1978
-
- Article
-
- You have access
- Export citation
The Stone-Weierstrass theorem for wallman rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 230-240
- Print publication:
- March 1978
-
- Article
-
- You have access
- Export citation
On generalizations of C*-embedding for wallman rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 215-229
- Print publication:
- March 1978
-
- Article
-
- You have access
- Export citation
Projecting and uniformising Borel sets with Kσ-sections II
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 233-246
- Print publication:
- December 1973
-
- Article
- Export citation
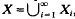 with each set
with each set