Refine listing
Actions for selected content:
95 results in 54Cxx
BARRELLED SPACES WITH(OUT) SEPARABLE QUOTIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 295-303
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
INVERSE LIMITS IN THE CATEGORY OF COMPACT HAUSDORFF SPACES AND UPPER SEMICONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 22 March 2013, pp. 49-59
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ON A THEOREM OF ARVANITAKIS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 250-256
- Print publication:
- January 2013
-
- Article
- Export citation
A NOTE ON RELATIVE PSEUDOCOMPACTNESS IN THE CATEGORY OF FRAMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 May 2012, pp. 120-130
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
A NOTE ON PARACOMPACT p-SPACES AND THE MONOTONE D-PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 463-469
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON CONTINUOUSLY URYSOHN SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 472-475
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
THE D-PROPERTY AND THE SORGENFREY LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 233-236
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
A WEAKLY ANALYTIC LOCALLY CONVEX SPACE WHICH IS NOT K-ANALYTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 31-35
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
EXTENSION OF CONTINUOUS MAPPINGS AND H1-RETRACTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 497-506
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A NOTE ON SPACES Cp(X)K-ANALYTIC-FRAMED IN ℝX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 141-146
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Products of Weak P-Spaces and K-Analytic Spaces
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 67-81
- Print publication:
- December 2007
-
- Article
- Export citation
Volterra spaces revisited
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-76
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
On Banach-Mazur compacta
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 316-335
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
On properties of metrizable spaces X preserved by t-equivalence
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-279
- Print publication:
- December 2000
-
- Article
- Export citation
On the Stone-Čech bicompactification of a bispace
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 358-372
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
A remark on C-compact spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-328
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Some properties of quasiuniform multifunction spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-177
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Algebraic characterizations of locally compact groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-420
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Stability of production economies
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 162-170
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
Universal and proximately universal limits
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 96-105
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
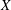
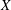
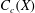
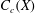
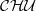
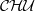
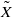 be the minimal dense linearly ordered extension of
be the minimal dense linearly ordered extension of 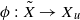 , ϕ(〈
, ϕ(〈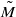 is a paracompact
is a paracompact 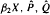 ) of the bispace (X, P, Q). We show that the ring of all continuous real-valued functions on (
) of the bispace (X, P, Q). We show that the ring of all continuous real-valued functions on (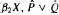 ) may be identified with the uniform closure of a suitable subring of
) may be identified with the uniform closure of a suitable subring of 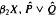 ). Using this result, we give a characterization of the Wallman-Sanin compactifications of the pairwise Tychonoff bitopological spaces.
). Using this result, we give a characterization of the Wallman-Sanin compactifications of the pairwise Tychonoff bitopological spaces.