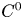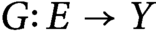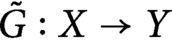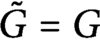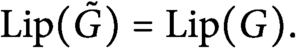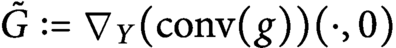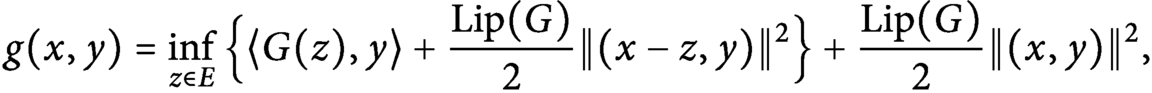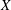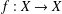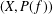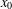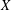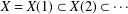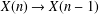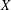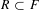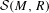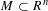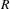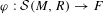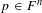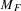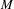Refine listing
Actions for selected content:
95 results in 54Cxx
Continuous flows generate few homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 25 August 2020, pp. 971-983
-
- Article
- Export citation
PROOFS OF URYSOHN’S LEMMA AND THE TIETZE EXTENSION THEOREM VIA THE CANTOR FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 03 July 2020, pp. 326-332
- Print publication:
- April 2021
-
- Article
- Export citation
Kirszbraun’s Theorem via an Explicit Formula
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 April 2020, pp. 142-153
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
FINITENESS OF TOPOLOGICAL ENTROPY FOR LOCALLY COMPACT ABELIAN GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 81-105
- Print publication:
- January 2021
-
- Article
- Export citation
Separable Quotients of Free Topological Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 29 November 2019, pp. 610-623
- Print publication:
- September 2020
-
- Article
- Export citation
Topological entropy of Markov set-valued functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 24 September 2019, pp. 321-337
- Print publication:
- February 2021
-
- Article
- Export citation
Fixed points of multivalued maps under local Lipschitz conditions and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1467-1494
- Print publication:
- June 2020
-
- Article
- Export citation
HOMOTOPY TYPES OF GAUGE GROUPS OVER NON-SIMPLYCONNECTED CLOSED 4-MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 349-371
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
CONTINUITY ON GENERALISED TOPOLOGICAL SPACES VIA HEREDITARY CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 21 February 2018, pp. 320-330
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
A UNIFIED APPROACH TO CONTINUOUS, MEASURABLE SELECTIONS, AND SELECTIONS FOR HYPERSPACES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 607-627
- Print publication:
- 2018
-
- Article
- Export citation
HOMOGENEOUS FUNCTIONALLY ALEXANDROFF SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 331-339
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ON FUNCTIONS ATTRACTING POSITIVE ENTROPY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 69-79
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
The Inner Corona Algebra of a C 0(X)-Algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 299-318
-
- Article
- Export citation
METRIC REGULARITY—A SURVEY PART II. APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 376-417
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Extension of de Bruijn's identity to dependent non-Gaussian noise channels
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 360-368
- Print publication:
- June 2016
-
- Article
- Export citation
LIPSCHITZ RETRACTION OF FINITE SUBSETS OF HILBERT SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 146-151
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Diagonals of Separately Absolutely Continuous Mappings Coincide with the Sums of Absolutely Convergent Series of Continuous Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 435-444
-
- Article
- Export citation
CARDINALITY OF INVERSE LIMITS WITH UPPER SEMICONTINUOUS BONDING FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 23 September 2014, pp. 167-174
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Subexponential class group and unit group computation in large degree number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 385-403
-
- Article
-
- You have access
- Export citation
ON THE SUBSTITUTION THEOREM FOR RINGS OF SEMIALGEBRAIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 01 July 2014, pp. 857-894
- Print publication:
- October 2015
-
- Article
- Export citation