We give new presentations of the five Mathieu groups, the simple groups J1, J2, HS, McL, Co3, and some other simple and related groups. All generators in these presentations are involutions. Our presentations are simpler than the known presentations of this type for the groups mentioned above.

We study the embeddings of a finite p-group U into Sylow p-subgroups of Sym (U) induced by the right regular representation p: U→ Sym(U). It turns out that there is a one-to-one correspondence between the chief series in U and the Sylow p-subgroups of Sym (U) containing Up. Here, the Sylow p-subgroup Pσ of Sym (U) correspoding to the chief series σ in U is characterized by the property that the intersections of Up with the terms of any chief series in Pσ form σp. Moreover, we see that p: U→ Pσ are precisely the kinds of embeddings used in a previous paper to construct the non-trivial countable algebraically closed locally finite p-groups as direct limits of finite p-groups.

We determine all conjugacy classes of maximal local subgroups of Thompson's sporadic simple group, and all maximal non-local subgroups except those with socle isomorphic to one of five particular small simple groups.

We determine all conjugacy classes of maximal p-local subgroups of the Monster for p ≠ 2.

It is proved that a finite soluble group of order n has at most (n − 1)/(q − 1) maximal subgroups, where q is the smallest prime divisor of n.

A group G is called normally (subnormally) detectable if the only normal (subnormal) subgroups in any direct product G1 × … × Gn of copies of G are just the direct factors Gi. We give an internal characterization of finite subnormally detectable groups and obtain analogous results for associative rings and for Lie algebras. The main part of the paper deals with a study of normally detectable groups, where we verify a conjecture of T. O. Hawkes in a number of special cases.

In this paper the question is considered of when the wreath product of a nilpotent group with a CLT group G is a CLT group. It is shown that if the field with Pr elements is a splitting field of a Hall P1–subgroup of G, then P wr G is a CLT group for all p–groups P with |P/P1|≥ pr. Moreover, the class of all groups G having the property that N wr G is a CLT group for every nilpotent group N is shown to be quite large. For exmple, every group of odd order can be embedded as a subgroup of a group belonging to this class.

We discuss intersections of subnormal subgroups and formation projectors in finite (not necessarily soluble) groups.

A technique is described for calculating the number of block ideals of FG, where F is a algebraically closed field of characteristic p, and where G is a p-soluble finite group. Among its consequences are the following: if U is a G-invariant irreducible FOp′(G)-module, then there is a unique block ideal of FG whose restriction to Op′(G) has all its composition factors isomorphic to U; and if G has p′-length 1, the number of block ideals of FG is the number of G-conjugacy classes of Op′(G)

An infinite family of 2-groups is produced. These groups have no direct factors and have a non-abelian automorphism group in which all automorphisms are central.

Let G be a p–group with cyclic L(G) = Z. Then L(G) = {Z < H ≦ G|H′ ∩ Z = (1)}, a poset ordered under inclusion. Then the associated simplicial complex |L(G)| is homotopic to a bouquet of spheres. A subgroup E of G is called a CES if CG (E) = Z = L(E) and if E/Z is elementary. Then |L(G)| is homotopic to the one-point union of the |L(E)| for all CES's E in G. If |E/Z| = p2n then |L(E)| is homotopic to a one-point union of pn2 (n– 1)-spheres.

In this paper periodic modules over group rings and algebras are considered. A new lower bound for the p-part of the rank of a periodic module with abeian vertex is given, and results on periodic modules with odd/even and small periods are obtained. In particular, it is shown that characters afforded by periodic lattices of odd period satisfy strong properties and that irreducible periodic lattices are always of even period.

Gaschütz has introduced the concept of a product of a Schunck class and a (saturated) formation (differing from the usual product of classes) and has shown that this product is a Schunck class provided that both of its factors consist of finite soluble groups. We investigate the same question in the context of arbitrary finite groups.

In this note we characterize PSL2(7) by conditions on the order of the group and the orders of its elements.

We define and investigate H-prefrattini subgroups for Schunck classes H of finite soluble groups, and solve a problem of Gaschütz concerning the structure of H-prefrattini groups for H = {1}.

In this note a formation U is considered which can be defined by a sequence of laws which ‘almost’ hold in every finite supersoluble group. The class U contains all finite supersoluble groups and each group in U has a Sylow tower.

It is shown that a finite group belongs to U if and only if all of its subgroups with nilpotent commutator subgroup are supersoluble. A more general result concerning classes of this type finally proves that U is a saturated formation.

Suppose the elementary abelian group A acts on the group G where A and G have relatively prime orders. If CG(a) belongs to some formation F for all non-identity elements a in A, does it follow that G belongs to F? For many formations, the answer is shown to be yes provided that the rank of A is sufficiently large.

Let G be a cyclic group of prime order p and K a field of characteristic p. The set of classes of isomorphic indecomposable (K, G)-modules forms a basis over the complex field for an algebra p (Green, 1962) with addition and multiplication being derived from direct sum and tensor product operations.

Algebras n with similar properties can be defined for all n ≥ 2. Each such algebra is isomorphic to a matrix algebra Mn of n × n matrices with complex entries and standard operations. The characters of elements of n are the eigenvalues of the corresponding matrices in Mn.

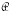
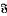The Fitting class (of finite, soluble, groups), , is said to be Hall π-closed (where π is a set of primes) if whenever 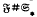G is a group in and H is a Hall π-subgroup of G, then H belongs to . In this paper, we study the Hall π-closure of products of Fitting classes. Our main result is a characterisation of the Hall π-closedFitting classes of the form (where 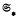denotes the so-called smallest normal Fitting class), subject to a restriction connecting π with the characteristic of 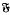. We also characterise those Fitting classes 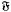(respectively, 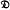) such that 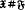(respectively, 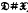) is Hall π-closed for all Fitting classes 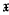. In each case, part of the proof uses a concrete group construction. As a bonus, one of these construction also yields a “cancellation result” for certain products of Fitting classes.

Every irreducible ordinary character in a p-block of a finite metabelian group is of height 0 if and only if the defect group of the p-block is abelian.