Refine listing
Actions for selected content:
616 results in 20Cxx
Nilpotent groups are not dualizable
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-180
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Orbit sizes, local subgroups and chains of p-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 325-338
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Multiplicity-free quotient tensor algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-298
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Young modules for symmetric groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-210
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Lie powers of free modules for certain groups of prime power order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-158
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
A note on minimal coverings of groups by subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-168
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Restricted Lazard elimination and modular Lie powers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 259-278
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Cyclic permutable subgroups of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-176
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Ensuring commutativity of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-234
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Nilpotency indices of the radicals of finite p-solvable group algebras, I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 117-133
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
The structure of finite groups in which permutability is a transitive relation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-160
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Finite dinilpotent groups of small derived length
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 3 / December 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 318-328
- Print publication:
- December 1999
-
- Article
-
- You have access
- Export citation
Some questions about p-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 3 / December 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 356-379
- Print publication:
- December 1999
-
- Article
-
- You have access
- Export citation
Enumerating p-Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 191-205
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Free Lie algebras as modules for symmetric groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-156
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Bounds in the restricted Burnside problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 261-271
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Partial characters with respect to a normal subgroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 104-124
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Finite groups that need more generators than any proper quotient
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 82-91
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
A family of dominant Fitting classes of finite soluble groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-43
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
The number of blocks with a given defect group
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 368-373
- Print publication:
- December 1997
-
- Article
- Export citation
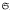 , of all permutations of a free generating set of
, of all permutations of a free generating set of 