Refine listing
Actions for selected content:
616 results in 20Cxx
Fitting classes based on groups of nilpotent length three with operator-isomorphic minimal normal subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 3 / December 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 448-467
- Print publication:
- December 1991
-
- Article
-
- You have access
- Export citation
Groups of odd order in which every subnormal subgroup has defect at most two
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-342
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
Integral and p-modular semisimple deformations for p-solvable groups of finite representation type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-232
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Static modules and non-normal Clifford theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 347-353
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
On tensor induction of group representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 486-501
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
Lie rings of groups of prime exponent
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 386-398
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
Stably free resolutions of lattices over finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-385
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
Centralizing properties in simple locally finite groups and large finite classical groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 502-513
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
A character-theory-free characterization of the Mathieu group M12
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-230
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Allgemeines Über Äussere Fittingpaare
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-249
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Finite groups which admit a fixed-point-free automorphism group isomorphic to S3
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-396
- Print publication:
- June 1990
-
- Article
-
- You have access
- Export citation
Subgroups of the Schur multiplier
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 497-505
- Print publication:
- June 1990
-
- Article
-
- You have access
- Export citation
On finite ρ-groups with isomorphic maximal subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-213
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
On presentation of PSL (2, pn)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 333-346
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
Monomial representations and generalizations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 264-280
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
Hypernormalizing groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-225
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
Maximal subgroups and the Jordan-Hölder Theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 356-364
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
A self-centralizing characteristic subgroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 302-307
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
Projective characters of degree one and the inflation-restriction sequence
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 272-280
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
Subnormal embedding of relatively complete groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 3 / December 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 389-400
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
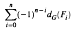 where
where