Refine listing
Actions for selected content:
616 results in 20Cxx
An extension theorem for integral representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-15
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Lattice embeddings of abelian prime power groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 259-278
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
More generalised Sylow theorems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 1 / February 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 84-92
- Print publication:
- February 1997
-
- Article
-
- You have access
- Export citation
Bases for induced characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-376
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
The modular group algebra problem for groups of order p5
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-237
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
A Hall-type closure property for certain Fitting classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 204-213
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
On p-groups whose maximal subgroups are isomorphic
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-147
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
On the faithful representations, of degree 2n, of certain extensions of 2-groups by orthogonal and symplectic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-247
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
On the number of subgroups in finite solvable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-141
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
A particular class of supersoluble groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-364
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
A non-coprime Hall-Higman reduction theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-137
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
The nuclear length of a character
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 49-59
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
The π-character theory of solvable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-102
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Coverings and coverings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-128
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Extensions of G-posets and Quillen's complex
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 60-75
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Testing modules for irreducibility
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-16
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Metabelian Lie powers of group representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-168
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Central idempotents in p-adic group rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 278-289
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
On minimal Fitting classes of periodic, infinite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 3 / June 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 304-320
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
Conjugacy classes of subgroups in p-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 294-303
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
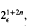 , or to the central product 4 o 2
, or to the central product 4 o 2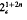 and powers of
and powers of 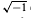 otherwise. This explicit description of a projective representation is useful for computing character values or computing with central extensions of
otherwise. This explicit description of a projective representation is useful for computing character values or computing with central extensions of 