Refine listing
Actions for selected content:
616 results in 20Cxx
Normalizers of 2-subgroups in black-box groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 307-319
-
- Article
-
- You have access
- Export citation
Constructing representations of Hecke algebras for complex reflection groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 426-450
-
- Article
-
- You have access
- Export citation
FINITE GROUPS WHOSE NONCENTRAL COMMUTING ELEMENTS HAVE CENTRALIZERS OF EQUAL SIZE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 07 July 2010, pp. 293-304
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF LATIN RECTANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 167-170
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
PARTIAL COMPLEMENTS IN FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 10 June 2010, pp. 1-7
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Constructing maximal subgroups of orthogonal groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 164-191
-
- Article
-
- You have access
- Export citation
A new construction of the Ree groups of type 2G2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 531-542
-
- Article
-
- You have access
- Export citation
SOLVABILITY OF FINITE GROUPS VIA CONDITIONS ON PRODUCTS OF 2-ELEMENTS AND ODD p-ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 265-273
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ON FINITE p-GROUPS WITH SUBGROUPS OF BREADTH 1
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 12 April 2010, pp. 84-98
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Character tables of the maximal parabolic subgroups of the Ree groups 2F4(q2)
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 April 2010, pp. 90-110
-
- Article
-
- You have access
- Export citation
On the minimal ramification problem for ℓ-groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 18 March 2010, pp. 599-606
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
The character table of a group of shape (2×2.G):2
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 March 2010, pp. 82-89
-
- Article
-
- You have access
- Export citation
The group of endotrivial modules for the symmetric and alternating groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 83-95
-
- Article
-
- You have access
- Export citation
GROUPS WITH ABELIAN SYLOW SUBGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 16 December 2009, pp. 43-47
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
On some modular representations of the Borel subgroup of GL2(Qp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 58-80
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF PRIME ORDER SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 329-357
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
GROUP ALGEBRAS WHOSE GROUP OF UNITS IS POWERFUL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 325-328
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Whittaker unitary dual of affine graded Hecke algebras of type E
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1563-1616
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
Leading coefficients and cellular bases of Hecke algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 653-677
-
- Article
-
- You have access
- Export citation
OVERGROUPS OF PRIMITIVE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 01 August 2009, pp. 37-82
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
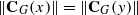 . Applying results of Schmidt [‘Zentralisatorverbände endlicher Gruppen’,
. Applying results of Schmidt [‘Zentralisatorverbände endlicher Gruppen’, 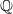 with no more than
with no more than 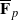 -representation
-representation 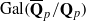 by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(
by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(