Refine listing
Actions for selected content:
616 results in 20Cxx
TOPOLOGY OF THE REPRESENTATION VARIETIES WITH BOREL MOLD FOR UNSTABLE CASES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 11 October 2011, pp. 55-87
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Computing character tables of groups of type M.G.A
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 173-178
-
- Article
-
- You have access
- Export citation
THE CLASSIFICATION OF SOME MODULAR FROBENIUS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 25 July 2011, pp. 11-18
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ON B(5,k) GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 13 July 2011, pp. 393-407
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Factorization of the canonical bases for higher-level Fock spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 20 June 2011, pp. 23-51
-
- Article
-
- You have access
- Export citation
Alternating units as free factors in the group of units of integral group rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 695-709
-
- Article
-
- You have access
- Export citation
Gaudin subalgebras and stable rational curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1463-1478
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Module structure on Lie powers and natural coalgebra-split sub-Hopf algebras of tensor algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 04 April 2011, pp. 467-504
-
- Article
-
- You have access
- Export citation
ON NONNILPOTENT SUBSETS IN GENERAL LINEAR GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 01 April 2011, pp. 369-375
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Groups with few conjugacy classes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 31 March 2011, pp. 423-430
-
- Article
-
- You have access
- Export citation
On conditional permutability and saturated formations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 309-319
-
- Article
-
- You have access
- Export citation
Primitivity testing of finite nilpotent linear groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 March 2011, pp. 87-98
-
- Article
-
- You have access
- Export citation
Is the function field of a reductive Lie algebra purely transcendental over the field of invariants for the adjoint action?
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 01 February 2011, pp. 428-466
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Fixed-point free action of an abelian group of odd non-squarefree exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 77-89
-
- Article
-
- You have access
- Export citation
LIFTS OF PARTIAL CHARACTERS WITH CYCLIC DEFECT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 November 2010, pp. 145-163
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
A CONDITION IN FINITE SOLVABLE GROUPS RELATED TO CYCLIC SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 267-272
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
CENTRES OF SYMMETRIC CELLULAR ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 14 September 2010, pp. 511-522
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
The Alperin weight conjecture and Uno’s conjecture for the Monster 𝕄, p odd
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 27 August 2010, pp. 320-356
-
- Article
-
- You have access
- Export citation
A Satake isomorphism in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 23 August 2010, pp. 263-283
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Rationality and Sylow 2-subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 787-798
-
- Article
-
- You have access
- Export citation
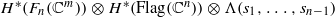 are isomorphic as algebras. Here the degree of
are isomorphic as algebras. Here the degree of  and
and  . They correspond to
. They correspond to  and
and  -module structures. We establish that the transition matrices relating these two bases are unitriangular with coefficients in ℕ[
-module structures. We establish that the transition matrices relating these two bases are unitriangular with coefficients in ℕ[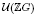 , the group of units of ℤ
, the group of units of ℤ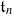 . We show that Gaudin subalgebras form a variety isomorphic to the moduli space
. We show that Gaudin subalgebras form a variety isomorphic to the moduli space 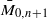 of stable curves of genus zero with
of stable curves of genus zero with 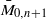 in a Grassmannian of (
in a Grassmannian of (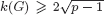 with equality if and only if if
with equality if and only if if 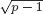 is an integer,
is an integer, 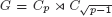 and
and 