Refine listing
Actions for selected content:
616 results in 20Cxx
SOME NEW CHARACTERISATIONS OF FINITE
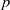 $p$-SUPERSOLUBLE GROUPS
$p$-SUPERSOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 08 November 2013, pp. 514-521
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Computing characters of groups with central subgroups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 07 November 2013, pp. 398-406
-
- Article
-
- You have access
- Export citation
MIXING FOR PROGRESSIONS IN NONABELIAN GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 29 August 2013, e2
-
- Article
-
- You have access
- Open access
- Export citation
SPECIAL MAXIMAL SUBGROUPS OF
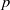 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 415-419
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Shifted generic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 1765-1788
- Print publication:
- October 2013
-
- Article
- Export citation
PRIMITIVE SUBGROUPS AND PST-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 373-378
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
CONCISENESS OF COPRIME COMMUTATORS IN FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 252-258
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Fusion systems and group actions with abelian isotropy subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 873-886
-
- Article
-
- You have access
- Export citation
Intersecting families in classical Coxeter groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 887-908
-
- Article
-
- You have access
- Export citation
ON CONJUGACY OF SUPPLEMENTS OF NORMAL SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 293-299
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ON NONINNER AUTOMORPHISMS OF FINITE NONABELIAN
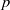 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 June 2013, pp. 202-209
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
A SOLVABILITY CRITERION FOR FINITE LOOPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 30 April 2013, pp. 92-96
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ON HUPPERT’S CONJECTURE FOR THE CONWAY AND FISCHER FAMILIES OF SPORADIC SIMPLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 11 April 2013, pp. 289-303
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
On bar lengths in partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 535-550
-
- Article
-
- You have access
- Export citation
ON THE
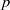 $p$-LENGTH AND THE WIELANDT LENGTH OF A FINITE
$p$-LENGTH AND THE WIELANDT LENGTH OF A FINITE 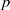 $p$-SOLUBLE GROUP
$p$-SOLUBLE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 March 2013, pp. 453-459
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
COMMUTATIVITY DEGREE OF A CLASS OF FINITE GROUPS AND CONSEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 30 January 2013, pp. 448-452
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
CONJUGACY CLASS SIZE CONDITIONS WHICH IMPLY SOLVABILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 15 January 2013, pp. 297-300
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
2-subnormal quadratic offenders and Oliver's p-group conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 10 December 2012, pp. 211-222
-
- Article
-
- You have access
- Export citation
Splitting fusion systems over 2-groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 263-301
-
- Article
-
- You have access
- Export citation
S3-free 2-fusion systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 27-48
-
- Article
-
- You have access
- Export citation
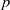
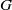
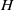
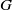
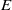
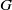
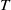
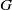
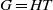
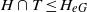
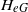
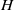
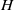
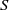
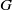
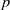
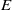
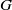
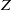
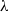
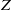
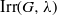
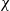
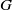
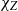
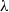
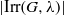
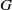
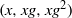
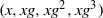
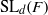
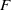
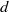
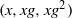
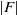
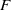
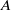
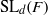
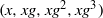
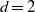
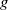
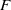
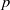
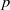
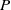

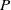

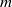
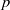
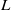
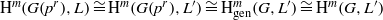
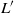
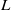
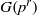
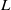
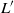
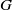
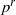
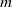
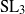
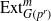
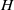
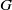
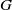
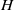
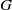
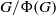
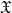
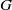
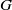
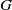
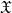
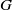
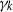
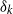
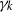
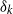
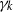
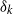
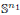 × … ×
× … × 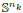 for some positive integers
for some positive integers 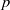
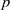
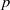
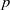
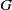
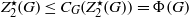
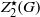
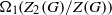
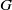
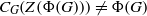
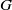
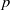
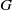
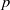
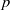
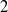
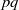
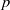
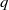
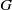
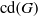
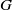
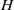
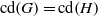
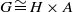
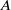
 . The proof involves a recent similar result for partitions, proved by Bessenrodt and the authors.
. The proof involves a recent similar result for partitions, proved by Bessenrodt and the authors.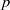
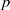
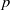
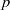
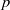
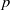
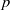
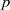
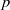
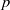
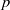
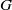
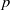
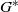
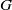
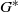
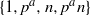
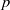

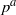

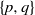
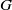
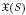 contains the Thompson subgroup
contains the Thompson subgroup 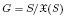 has class at most log
has class at most log