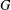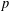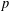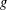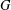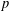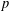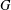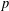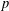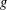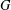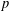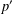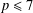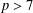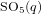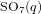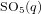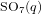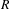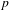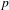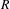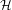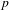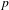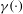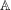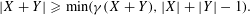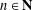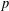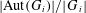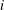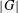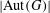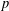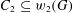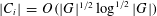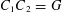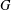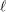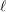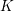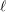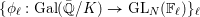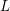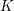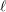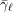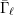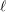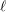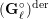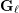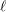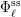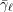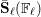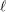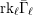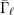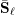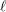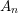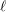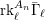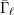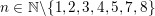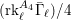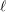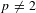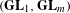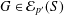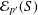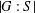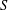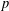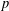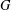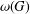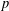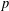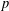Refine listing
Actions for selected content:
616 results in 20Cxx
NONVANISHING ELEMENTS FOR BRAUER CHARACTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 August 2015, pp. 96-107
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
LARGE P-GROUPS WITHOUT PROPER SUBGROUPS WITH THE SAME DERIVED LENGTH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 23 July 2015, pp. 445-459
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
ON NONCOMMUTING SETS AND CENTRALISERS IN INFINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 42-46
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
THE SUBGROUP COMMUTATIVITY DEGREE OF FINITE
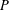 $P$-GROUPS
$P$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 37-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Restricting unipotent characters in special orthogonal groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 July 2015, pp. 456-488
-
- Article
-
- You have access
- Export citation
THE WORK OF L. G. KOVÁCS ON REPRESENTATION THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 16 June 2015, pp. 34-42
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
THE MOONSHINE MODULE FOR CONWAY’S GROUP
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 15 June 2015, e10
-
- Article
-
- You have access
- Open access
- Export citation
Triple Factorizations and Supersolubility of Finite Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 11 June 2015, pp. 301-309
-
- Article
- Export citation
L. G. KOVÁCS’ WORK ON LIE POWERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 09 June 2015, pp. 9-19
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
THE PRO-p-IWAHORI HECKE ALGEBRA OF A REDUCTIVE p-ADIC GROUP III (SPHERICAL HECKE ALGEBRAS AND SUPERSINGULAR MODULES)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 03 June 2015, pp. 571-608
- Print publication:
- June 2017
-
- Article
- Export citation
CAUCHY–DAVENPORT TYPE THEOREMS FOR SEMIGROUPS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 May 2015, pp. 1-12
- Print publication:
- 2016
-
- Article
- Export citation
AN APPROACH TO CAPABLE GROUPS AND SCHUR’S THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 05 May 2015, pp. 52-56
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
FINITE
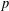 $p$-GROUPS WITH SMALL AUTOMORPHISM GROUP
$p$-GROUPS WITH SMALL AUTOMORPHISM GROUP
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 20 April 2015, e7
-
- Article
-
- You have access
- Open access
- Export citation
Champ: a Cherednik algebra Magma package
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 266-307
-
- Article
-
- You have access
- Export citation
A REFINED WARING PROBLEM FOR FINITE SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 17 March 2015, e6
-
- Article
-
- You have access
- Open access
- Export citation
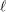 $\ell$-independence for compatible systems of (mod
$\ell$-independence for compatible systems of (mod 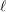 $\ell$) representations
$\ell$) representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 02 March 2015, pp. 1215-1241
- Print publication:
- July 2015
-
- Article
- Export citation
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 18 February 2015, pp. 625-671
- Print publication:
- July 2016
-
- Article
- Export citation
THE NUMBER OF PROFINITE GROUPS WITH A SPECIFIED SYLOW SUBGROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 19 January 2015, pp. 108-127
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
CHARACTER TABLES OF METACYCLIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 387-400
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
ON THE
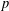 $p$-LENGTH AND THE WIELANDT SERIES OF A FINITE
$p$-LENGTH AND THE WIELANDT SERIES OF A FINITE 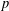 $p$-SOLUBLE GROUP
$p$-SOLUBLE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 09 December 2014, pp. 219-226
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation