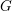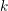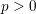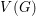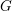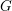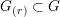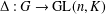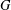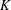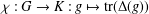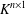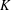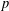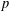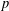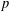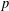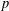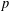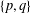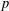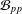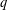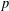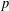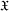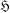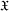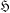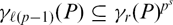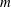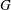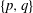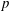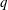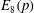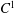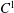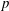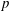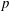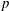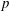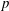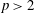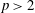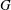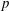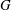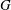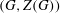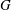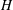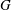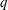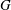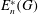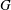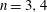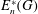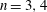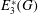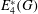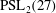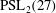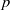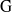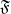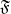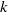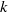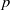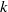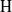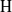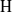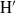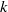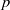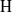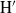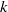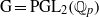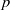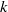Refine listing
Actions for selected content:
616 results in 20Cxx
Support varieties for rational representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 13 November 2014, pp. 765-792
- Print publication:
- April 2015
-
- Article
- Export citation
DETERMINING ASCHBACHER CLASSES USING CHARACTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 355-363
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
SOME PROPERTIES OF SEMI-ABELIAN
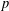 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 15 October 2014, pp. 86-91
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
ON SETS OF PP-GENERATORS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 241-249
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
ESTIMATION AND COMPUTATION WITH MATRICES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 175-176
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
WORDS AND PRONILPOTENT SUBGROUPS IN PROFINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 29 September 2014, pp. 343-364
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
CONDITIONS FOR A SCHUNCK CLASS TO BE A FORMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 69-75
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A BOUND ON THE p-LENGTH OF P-SOLVABLE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 26 August 2014, pp. 167-171
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
Subexponential class group and unit group computation in large degree number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 385-403
-
- Article
-
- You have access
- Export citation
SOLVABILITY OF FINITE GROUPS WITH FOUR CONJUGACY CLASS SIZES OF CERTAIN ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 21 July 2014, pp. 250-256
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Rational rigidity for
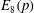 ${E}_{8}(p)$
${E}_{8}(p)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1679-1702
- Print publication:
- October 2014
-
- Article
- Export citation
Sur les rapprochements par conjugaison en dimension 1 et classe
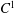 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 19 June 2014, pp. 1183-1195
- Print publication:
- July 2014
-
- Article
- Export citation
The
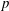 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 1125-1168
- Print publication:
- July 2014
-
- Article
- Export citation
NONINNER AUTOMORPHISMS OF ORDER
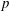 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ IN FINITE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ IN FINITE 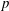 $p$-GROUPS OF COCLASS 2, WHEN
$p$-GROUPS OF COCLASS 2, WHEN 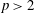 $p>2$
$p>2$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 232-236
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON THE FORMAL AFFINE HECKE ALGEBRA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 09 June 2014, pp. 837-855
- Print publication:
- October 2015
-
- Article
- Export citation
ON NONINNER 2-AUTOMORPHISMS OF FINITE 2-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 29 May 2014, pp. 227-231
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON A CLASS OF SUPERSOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 23 May 2014, pp. 220-226
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF P. HALL FOR ENGEL WORDS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 13 May 2014, pp. 237-246
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Classification of subgroups isomorphic to
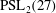 $\mathrm{PSL}_2(27)$ in the Monster
$\mathrm{PSL}_2(27)$ in the Monster
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 33-46
-
- Article
-
- You have access
- Export citation
Pro-
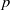 $\lowercase p$ Iwahori–Hecke algebras are Gorenstein
$\lowercase p$ Iwahori–Hecke algebras are Gorenstein
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 28 November 2013, pp. 753-809
- Print publication:
- October 2014
-
- Article
- Export citation