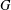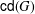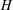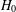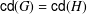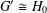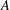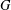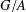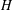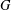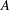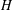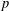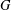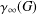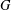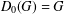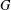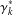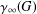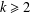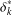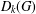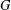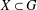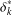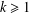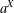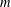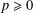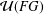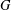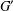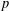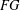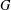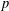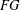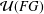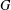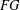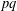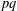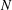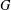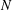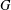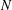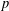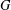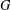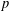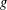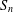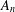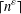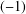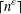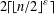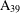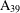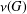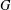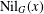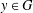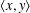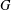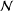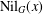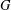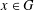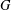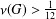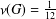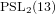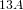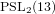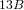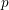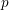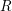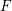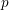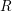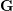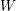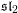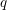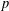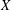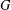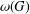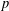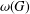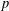Refine listing
Actions for selected content:
616 results in 20Cxx
GROUPS WITH THE SAME CHARACTER DEGREES AS SPORADIC ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 254-265
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
REALIZABILITY PROBLEM FOR COMMUTING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 335-355
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
COCHAIN SEQUENCES AND THE QUILLEN CATEGORY OF A COCLASS FAMILY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 185-204
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Double affine Hecke algebras and generalized Jones polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1333-1384
- Print publication:
- July 2016
-
- Article
- Export citation
BOUNDING THE ORDER OF THE NILPOTENT RESIDUAL OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 273-277
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
GROUP ALGEBRAS WITH ENGEL UNIT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 244-252
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SYMMETRY CLASSES OF TENSORS ASSOCIATED TO NONABELIAN GROUPS OF ORDER
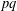 $pq$
$pq$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 36-42
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
NORMAL SUBGROUPS WHOSE CONJUGACY CLASS GRAPH HAS DIAMETER THREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 266-272
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ON THE TOTAL COMPONENT OF THE PARTIAL SCHUR MULTIPLIER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 374-402
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
A CHARACTER-THEORETIC CRITERION FOR THE SOLVABILITY OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 30-35
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
FINDING INVOLUTIONS WITH SMALL SUPPORT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 43-47
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A 2-ARC TRANSITIVE PENTAVALENT CAYLEY GRAPH OF
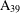 $\text{A}_{39}$
$\text{A}_{39}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 441-446
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Fusion Systems on Bicyclic 2-Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 989-1018
-
- Article
- Export citation
Bounding the Diameter of the Brauer Graph of a Block of a Solvable Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 591-603
-
- Article
- Export citation
ON THE PROBABILITY OF GENERATING NILPOTENT SUBGROUPS IN A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 447-453
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Every
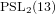 $\text{PSL}_{2}(13)$ in the Monster contains
$\text{PSL}_{2}(13)$ in the Monster contains 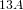 $13A$ -elements
$13A$ -elements
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 November 2015, pp. 667-674
-
- Article
-
- You have access
- Export citation
The pro-
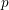 $p$-Iwahori Hecke algebra of a reductive
$p$-Iwahori Hecke algebra of a reductive 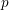 $p$-adic group I
$p$-adic group I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 23 October 2015, pp. 693-753
- Print publication:
- April 2016
-
- Article
- Export citation
The two-color Soergel calculus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 22 September 2015, pp. 327-398
- Print publication:
- February 2016
-
- Article
- Export citation
ON MAXIMAL SUBSETS OF PAIRWISE NONCOMMUTING ELEMENTS IN FINITE
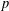 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 20 August 2015, pp. 380-389
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
ONE-DIMENSIONAL STOCHASTIC MODELS WITH OPEN BOUNDARIES: INTEGRABILITY, APPLICATIONS AND
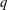 $q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
$q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 520-521
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation