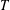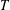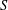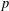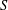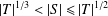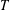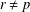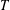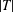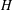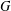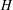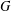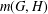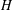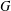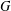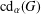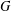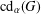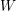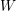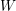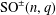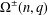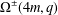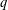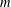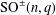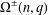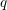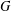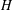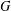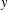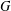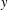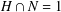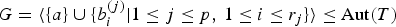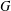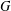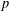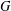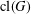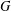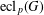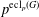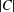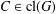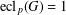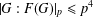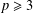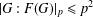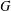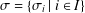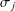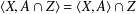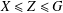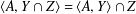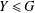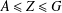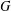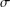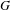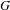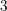Refine listing
Actions for selected content:
616 results in 20Cxx
On the First Zassenhaus Conjecture and Direct Products
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 15 October 2018, pp. 602-624
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Conditions for Sylow 2-subgroups of the Fixed Point Subgroup Implying Solubility
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 25 September 2018, pp. 211-220
-
- Article
- Export citation
Low Growth Equational Complexity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 25 September 2018, pp. 197-210
-
- Article
- Export citation
The HOMFLY-PT polynomials of sublinks and the Yokonuma–Hecke algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 18 September 2018, pp. 1269-1278
- Print publication:
- December 2018
-
- Article
- Export citation
ON THE SECOND-LARGEST SYLOW SUBGROUP OF A FINITE SIMPLE GROUP OF LIE TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 203-211
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
OVERGROUPS OF WEAK SECOND MAXIMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 83-88
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
PROJECTIVE CHARACTERS WITH PRIME POWER DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 78-82
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ON VANISHING CRITERIA THAT CONTROL FINITE GROUP STRUCTURE II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 251-257
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
ON CANONICAL BASES AND INDUCTION OF
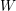 $W$-GRAPHS
$W$-GRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 17 July 2018, pp. 1-41
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
MODULAR DECOMPOSITION NUMBERS OF CYCLOTOMIC HECKE AND DIAGRAMMATIC CHEREDNIK ALGEBRAS: A PATH THEORETIC APPROACH
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 03 July 2018, e11
-
- Article
-
- You have access
- Open access
- Export citation
ON INVOLUTIONS AND INDICATORS OF FINITE ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 380-416
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
MULTIPLICATION FORMULAS AND SEMISIMPLICITY FOR
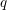 $q$-SCHUR SUPERALGEBRAS
$q$-SCHUR SUPERALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 98-126
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
A NOTE ON NORMAL COMPLEMENTS FOR FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 109-112
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Maximal Subgroups and Irreducible Representations of Generalized Multi-Edge Spinal Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 673-703
-
- Article
- Export citation
COCENTERS OF
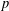 $p$ -ADIC GROUPS, I: NEWTON DECOMPOSITION
$p$ -ADIC GROUPS, I: NEWTON DECOMPOSITION
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 6 / 2018
- Published online by Cambridge University Press:
- 28 March 2018, e2
-
- Article
-
- You have access
- Open access
- Export citation
ON
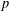 $p$ -PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS
$p$ -PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 406-411
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF FINITE PT-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 396-405
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Finite Groups Whose Common-Divisor Graph is Regular
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 329-341
-
- Article
- Export citation
RANK TWO TOPOLOGICAL AND INFINITESIMAL EMBEDDED JUMP LOCI OF QUASI-PROJECTIVE MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 15 February 2018, pp. 451-485
- Print publication:
- March 2020
-
- Article
- Export citation
SIMPLE MODULES IN THE AUSLANDER–REITEN QUIVER OF PRINCIPAL BLOCKS WITH ABELIAN DEFECT GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 05 February 2018, pp. 58-85
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
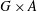
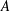
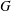


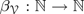
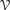 bounds the size of equation required to determine the membership of
bounds the size of equation required to determine the membership of 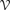 . Known examples of finitely generated varieties
. Known examples of finitely generated varieties 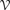 with unbounded equational complexity have growth in Ω(
with unbounded equational complexity have growth in Ω(