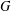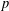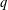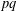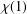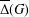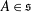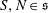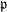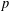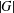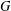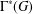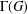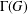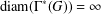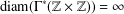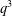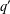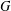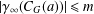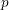Refine listing
Actions for selected content:
616 results in 20Cxx
MONOLITHIC BRAUER CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 434-439
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ON THE REGULARITY OF CHARACTER DEGREE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 08 March 2019, pp. 428-433
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Jordan–Chevalley Decomposition in Lie Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 28 February 2019, pp. 349-354
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ALGEBRAS OF GENERALIZED DIHEDRAL TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 181-236
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
Duality between p-groups with three characteristic subgroups and semisimple anti-commutative algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 25 February 2019, pp. 1827-1852
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Local duality for representations of finite group schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 424-453
- Print publication:
- February 2019
-
- Article
-
- You have access
- HTML
- Export citation
Reduced fusion systems over p-groups with abelian subgroup of index p: III
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1187-1239
- Print publication:
- June 2020
-
- Article
- Export citation
SQUARES OF DEGREES OF BRAUER CHARACTERS AND MONOMIAL BRAUER CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 58-60
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
THE GENERATING GRAPH OF INFINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 68-75
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Prime divisors of orders of products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1153-1162
- Print publication:
- October 2019
-
- Article
- Export citation
Two-color Soergel Calculus and Simple Transitive 2-representations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1523-1566
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Mixed Perverse Sheaves on Flag Varieties for Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1-55
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Degrees of Regular Sequences With a Symmetric Group Action
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 557-578
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Casselman’s Basis of Iwahori Vectors and Kazhdan–Lusztig Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1351-1366
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Unitary and Symmetric Units of a Commutative Group Algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 641-654
-
- Article
- Export citation
FITTING SUBGROUP AND NILPOTENT RESIDUAL OF FIXED POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 61-67
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
The Structure of Root Data and Smooth Regular Embeddings of Reductive Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 523-552
-
- Article
- Export citation
Fields of Definition for Representations of Associative Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 November 2018, pp. 291-304
-
- Article
- Export citation
ON THE GALOIS STRUCTURE OF ARITHMETIC COHOMOLOGY I: COMPACTLY SUPPORTED
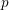 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 294-321
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
ON
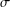 $\unicode[STIX]{x1D70E}$-QUASINORMAL SUBGROUPS OF FINITE GROUPS
$\unicode[STIX]{x1D70E}$-QUASINORMAL SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 413-420
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation