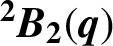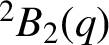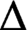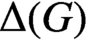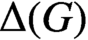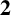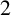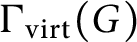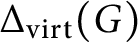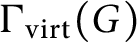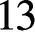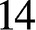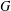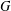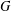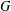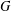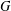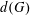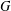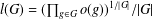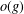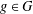Refine listing
Actions for selected content:
616 results in 20Cxx
IHARA LEMMA AND LEVEL RAISING IN HIGHER DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1701-1726
- Print publication:
- September 2022
-
- Article
- Export citation
COPRIME COMMUTATORS IN THE SUZUKI GROUPS
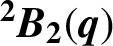 $^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
$^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 448-452
- Print publication:
- December 2021
-
- Article
- Export citation
ON ANALOGUES OF HUPPERT’S CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 272-277
- Print publication:
- October 2021
-
- Article
- Export citation
FINITE p-GROUPS AND COCLASS THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 164-166
- Print publication:
- August 2021
-
- Article
-
- You have access
- Export citation
A cancellation theorem for modules over integral group rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 27 November 2020, pp. 317-327
- Print publication:
- September 2021
-
- Article
- Export citation
THE CHARACTER GRAPH OF A FINITE GROUP IS PERFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 127-131
- Print publication:
- August 2021
-
- Article
- Export citation
THE INDUCTIVE BLOCKWISE ALPERIN WEIGHT CONDITION FOR TYPE
 ${\boldsymbol{\mathsf{C}}}$ AND THE PRIME
${\boldsymbol{\mathsf{C}}}$ AND THE PRIME 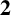 $\textbf{2}$
$\textbf{2}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 06 November 2020, pp. 1-20
- Print publication:
- August 2022
-
- Article
- Export citation
The virtually generating graph of a profinite group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 15 October 2020, pp. 808-819
- Print publication:
- December 2021
-
- Article
- Export citation
Variations on results on orders of products in finite groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 12 October 2020, pp. 1443-1449
- Print publication:
- October 2021
-
- Article
- Export citation
CONNECTIVITY PROPERTIES OF MCKAY QUIVERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 182-194
- Print publication:
- April 2021
-
- Article
- Export citation
BLOCKS WITH SMALL-DIMENSIONAL BASIC ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 461-474
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- Export citation
RATIONAL NEARLY SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 475-485
- Print publication:
- June 2021
-
- Article
- Export citation
On solvable groups with one vanishing class size
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 14 September 2020, pp. 1467-1486
- Print publication:
- October 2021
-
- Article
- Export citation
On semidirectly closed non-aperiodic pseudovarieties of finite monoids
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 24 August 2020, pp. 913-928
-
- Article
- Export citation
FINITE GROUPS WITH THE SAME JOIN GRAPH AS A FINITE NILPOTENT GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 640-650
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
A NOTE ON DERIVED LENGTH AND CHARACTER DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 13 July 2020, pp. 271-277
- Print publication:
- April 2021
-
- Article
- Export citation
On finite sets of small tripling or small alternation in arbitrary groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 30 June 2020, pp. 807-829
-
- Article
- Export citation
GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e32
-
- Article
-
- You have access
- Open access
- Export citation
FIRST-ORDER RECOGNIZABILITY IN FINITE AND PSEUDOFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 852-867
- Print publication:
- June 2020
-
- Article
- Export citation
PROPERTIES OF FINITE GROUPS DETERMINED BY THE PRODUCT OF THEIR ELEMENT ORDERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 June 2020, pp. 88-95
- Print publication:
- February 2021
-
- Article
- Export citation