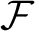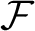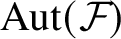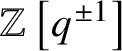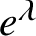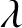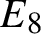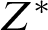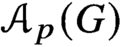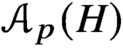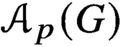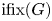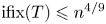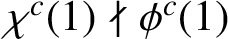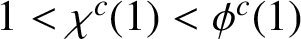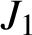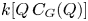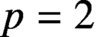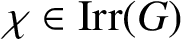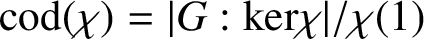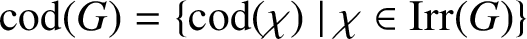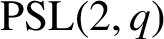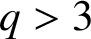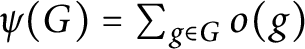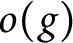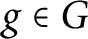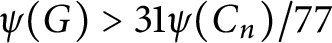Refine listing
Actions for selected content:
616 results in 20Cxx
Extensions of homomorphisms between localities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 14 September 2021, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON CERTAIN PRODUCTS OF PERMUTABLE SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 16 August 2021, pp. 278-285
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON HIGHER FROBENIUS–SCHUR INDICATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 12 July 2021, pp. 267-277
- Print publication:
- April 2022
-
- Article
- Export citation
Inverse K-Chevalley formulas for semi-infinite flag manifolds, I: minuscule weights in ADE type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 July 2021, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On class 2 quotients of linear groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 09 June 2021, pp. 590-593
-
- Article
- Export citation
SYMÉTRIES ET TRANSVEXIONS, PRINCIPALEMENT DANS LES GROUPES DE RANG DE MORLEY FINI SANS INVOLUTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 965-990
- Print publication:
- September 2021
-
- Article
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
On the involution fixity of simple groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 408-426
-
- Article
- Export citation
COMMUTATOR EQUATIONS IN FINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 320-335
- Print publication:
- May 2022
-
- Article
- Export citation
NONDIVISIBILITY AMONG IRREDUCIBLE CHARACTER CO-DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 68-74
- Print publication:
- February 2022
-
- Article
- Export citation
1324- and 2143-avoiding Kazhdan–Lusztig immanants and k-positivity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 14 May 2021, pp. 52-82
- Print publication:
- February 2023
-
- Article
- Export citation
ON THE RANK OF A VERBAL SUBGROUP OF A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 12 May 2021, pp. 145-159
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- Export citation
Brauer indecomposability of Scott modules with semidihedral vertex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 174-182
-
- Article
- Export citation
CONNECTED COMPONENTS IN THE INVARIABLY GENERATING GRAPH OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 25 March 2021, pp. 453-463
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
Rigid automorphisms of linking systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 March 2021, e23
-
- Article
-
- You have access
- Open access
- Export citation
THE CENTER OF SL2 TILTING MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 165-184
- Print publication:
- January 2022
-
- Article
- Export citation
The fields of values of characters of degree not divisible by p
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 February 2021, e2
-
- Article
-
- You have access
- Open access
- Export citation
AN ANALOGUE OF HUPPERT’S CONJECTURE FOR CHARACTER CODEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 February 2021, pp. 278-286
- Print publication:
- October 2021
-
- Article
- Export citation
Low-dimensional representations of finite orthogonal groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 26 January 2021, pp. 585-606
- Print publication:
- November 2021
-
- Article
- Export citation
On two conjectures about the sum of element orders
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 January 2021, pp. 30-38
- Print publication:
- March 2022
-
- Article
- Export citation