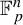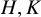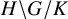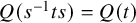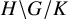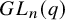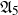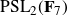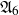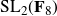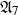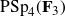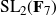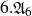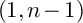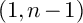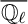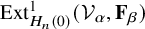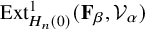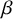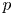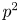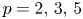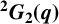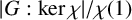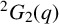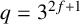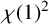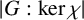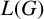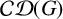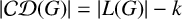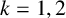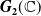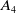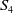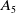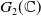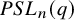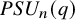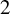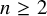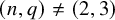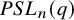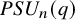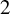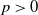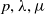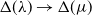Refine listing
Actions for selected content:
616 results in 20Cxx
ON LARGE ORBITS OF FINITE SOLVABLE GROUPS ON CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 07 February 2023, pp. 438-442
- Print publication:
- December 2023
-
- Article
- Export citation
On higher-order Fourier analysis in characteristic p
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 27 January 2023, pp. 3971-4040
- Print publication:
- December 2023
-
- Article
- Export citation
Double coset Markov chains
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite quasisimple groups acting on rationally connected threefolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 06 December 2022, pp. 531-568
- Print publication:
- May 2023
-
- Article
- Export citation
COHOMOLOGY OF THE BRUHAT–TITS STRATA IN THE UNRAMIFIED UNITARY RAPOPORT–ZINK SPACE OF SIGNATURE
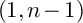 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 470-497
- Print publication:
- June 2023
-
- Article
- Export citation
Homological properties of 0-Hecke modules for dual immaculate quasisymmetric functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 October 2022, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Toward a classification of the supercharacter theories of Cp × Cp
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 990-1010
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RECOGNISING REE GROUPS
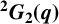 $\boldsymbol {{}^{2}G_{2}(q)}$ USING THE CODEGREE SET
$\boldsymbol {{}^{2}G_{2}(q)}$ USING THE CODEGREE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 28 September 2022, pp. 125-132
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE STABLE LIMIT DAHA AND THE DOUBLE DYCK PATH ALGEBRA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 26 September 2022, pp. 379-424
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Products of derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 September 2022, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME CRITERIA FOR SOLVABILITY AND NILPOTENCY OF FINITE GROUPS BY STRONGLY MONOLITHIC CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 120-124
- Print publication:
- August 2023
-
- Article
- Export citation
Kernels of localities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for surface groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 1850-1877
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SYLOW CLASSES OF REFLECTION SUBGROUPS AND PSEUDO-LEVI SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 508-510
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
FINITE GROUPS WITH ABNORMAL MINIMAL NONNILPOTENT SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 261-270
- Print publication:
- April 2023
-
- Article
- Export citation
FINITE GROUPS WITH LARGE CHERMAK–DELGADO LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 451-455
- Print publication:
- June 2023
-
- Article
- Export citation
Polyhedral groups in
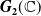 $\textbf{G}_{\textbf{2}}(\mathbb C)$
$\textbf{G}_{\textbf{2}}(\mathbb C)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 11 August 2022, pp. S123-S128
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of the groups
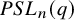 $PSL_n(q)$ and
$PSL_n(q)$ and 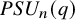 $PSU_n(q)$ by their
$PSU_n(q)$ by their 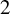 $2$-fusion systems, q odd
$2$-fusion systems, q odd
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 05 August 2022, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME PRODUCTS OF SUBGROUPS AND VANISHING CONJUGACY CLASS SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 271-275
- Print publication:
- April 2023
-
- Article
- Export citation
On homomorphisms into Weyl modules corresponding to partitions with two parts
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 272-283
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation