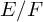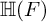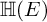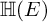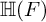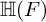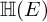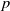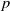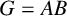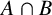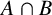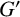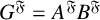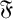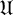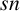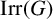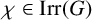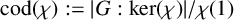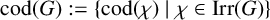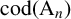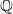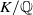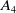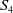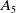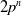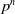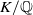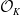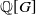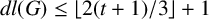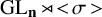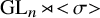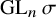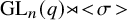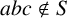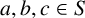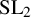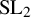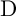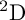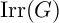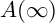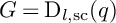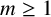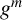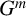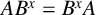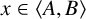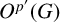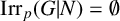Refine listing
Actions for selected content:
616 results in 20Cxx
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
- Print publication:
- January 2025
-
- Article
- Export citation
Affine Bruhat order and Demazure products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CHARACTERISATION OF SOLUBLE
 ${PST}$-GROUPS
${PST}$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 520-527
- Print publication:
- December 2024
-
- Article
- Export citation
PROJECTIVE CHARACTER VALUES ON REAL AND RATIONAL ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 514-519
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On twisted group ring isomorphism problem for p-groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 368-381
- Print publication:
- May 2024
-
- Article
- Export citation
GENERALISED MUTUALLY PERMUTABLE PRODUCTS AND SATURATED FORMATIONS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 30 January 2024, pp. 313-323
- Print publication:
- October 2024
-
- Article
- Export citation
ON THE CHARACTERISATION OF ALTERNATING GROUPS BY CODEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 115-120
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Leopoldt-type theorems for non-abelian extensions of
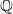 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLVABLE GROUPS WHOSE NONNORMAL SUBGROUPS HAVE FEW ORDERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 121-128
- Print publication:
- August 2024
-
- Article
- Export citation
E-Polynomials of Generic
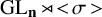 $\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
$\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMMON ZEROS OF IRREDUCIBLE CHARACTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 105-129
- Print publication:
- October 2024
-
- Article
- Export citation
ON EXTERIOR POWERS OF REFLECTION REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 90-102
- Print publication:
- August 2024
-
- Article
- Export citation
TRIPLE-PRODUCT-FREE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 129-135
- Print publication:
- August 2024
-
- Article
- Export citation
A combinatorial model for the transition matrix between the Specht and
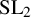 $\operatorname {SL}_2$-web bases
$\operatorname {SL}_2$-web bases
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 20 September 2023, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSIONS OF CHARACTERS IN TYPE D AND THE INDUCTIVE MCKAY CONDITION, I
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. 906-958
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH FEW NONPOWER SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 10 August 2023, pp. 529-540
- Print publication:
- June 2024
-
- Article
- Export citation
FINITE GROUPS WITH HEREDITARILY G-PERMUTABLE SCHMIDT SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 522-528
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE SOLVABLE TIDY GROUPS ARE DETERMINED BY HALL SUBGROUPS WITH TWO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 342-349
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON p-SOLVABILITY AND AVERAGE CHARACTER DEGREE IN A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 507-511
- Print publication:
- June 2024
-
- Article
- Export citation
Prime divisors and the number of conjugacy classes of finite groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-16
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation