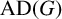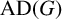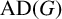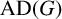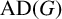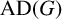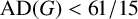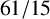Refine listing
Actions for selected content:
616 results in 20Cxx
On finite groups with bounded conjugacy classes of commutators
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-6
-
- Article
- Export citation
On the structures of the Johnson cokernels of the basis-conjugating automorphism groups of free groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-29
-
- Article
- Export citation
Derived equivalences for trigonometric double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE LARGEST CHARACTER DEGREE OF SOLVABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Splines on Cayley graphs of the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 June 2025, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Steiner Coset Partitions of Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1359-1373
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Character and class parameters from entries of character tables of symmetric groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 05 June 2025, pp. 439-447
- Print publication:
- September 2025
-
- Article
- Export citation
Functional degrees and arithmetic applications III: beyond prime exponent
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 30 May 2025, pp. 409-438
- Print publication:
- September 2025
-
- Article
- Export citation
On the Aldous-Caputo Spectral Gap Conjecture for Hypergraphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 259-298
- Print publication:
- September 2025
-
- Article
- Export citation
 $M_{p}$-GROUPS AND BRAUER CHARACTER DEGREES
$M_{p}$-GROUPS AND BRAUER CHARACTER DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 May 2025, pp. 1-5
-
- Article
- Export citation
Polishchuk’s conjecture and Kazhdan–Laumon representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 26 August 2025, pp. 993-1020
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exotic Fusion Systems Related to Sporadic Simple Groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 331-384
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Diagrammatics for the smallest quantum coideal and Jones–Wenzl projectors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-20
-
- Article
- Export citation
Quasi-polynomial representations of double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 April 2025, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A categorical action of the shifted
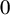 $0$-affine algebra
$0$-affine algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 April 2025, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KRONECKER CLASSES, NORMAL COVERINGS AND CHIEF FACTORS OF GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SMALL VALUES AND FORBIDDEN VALUES FOR THE FOURIER ANTI-DIAGONAL CONSTANT OF A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 297-316
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 869-897
-
- Article
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation