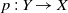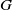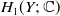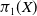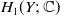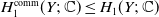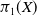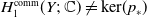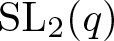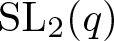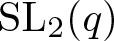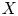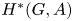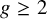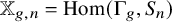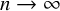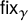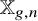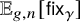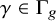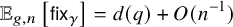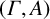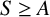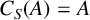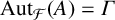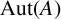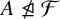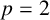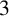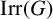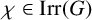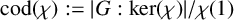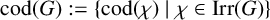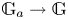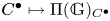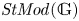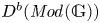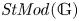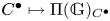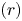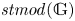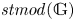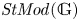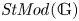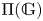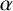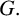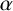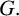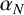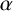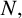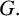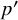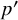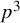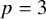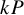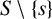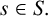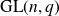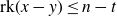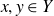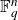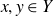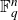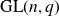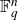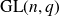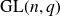Refine listing
Actions for selected content:
616 results in 20Cxx
Subrepresentations in the homology of finite covers of graphs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. 582-594
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weights in a Benson-Solomon block
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trivial source character tables of
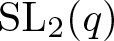 $\operatorname{SL}_2(q)$, part II
$\operatorname{SL}_2(q)$, part II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 689-709
-
- Article
- Export citation
LOCALLY FINITE SIMPLE GROUPS WHOSE NONNILPOTENT SUBGROUPS ARE PRONORMAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 512-521
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REAL BLOCKS WITH DIHEDRAL DEFECT GROUPS REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 14 June 2023, pp. 327-341
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Balmer spectrum of certain Deligne–Mumford stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. 1314-1346
- Print publication:
- June 2023
-
- Article
- Export citation
The Asymptotic Statistics of Random Covering Surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 May 2023, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-GROUPS WITH CYCLIC OR GENERALISED QUATERNION HUGHES SUBGROUPS: CLASSIFYING TIDY p-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 443-448
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONREALIZABILITY OF CERTAIN REPRESENTATIONS IN FUSION SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 257-288
- Print publication:
- April 2024
-
- Article
- Export citation
MODEL CATEGORIES AND PRO-p IWAHORI–HECKE MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1029-1076
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some products of finite groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 March 2023, pp. 89-99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CHARACTERISATION OF SPORADIC SIMPLE GROUPS BY CODEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 57-66
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Support varieties and stable categories for algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 27 March 2023, pp. 746-779
- Print publication:
- April 2023
-
- Article
- Export citation
HALL SUBGROUPS AND
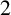 $2$-COCYCLE REGULARITY
$2$-COCYCLE REGULARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 24 March 2023, pp. 51-56
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRICT REGULARITY FOR
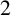 $2$-COCYCLES OF FINITE GROUPS
$2$-COCYCLES OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 24 March 2023, pp. 45-50
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of blocks with normal defect and abelian
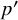 $p'$ inertial quotient
$p'$ inertial quotient
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 March 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE GROUPS WITH INDEPENDENT GENERATING SETS OF ONLY TWO SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 449-458
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersection theorems for finite general linear groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 129-160
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subsymmetric exchanged braids and the Burau matrix
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 154-187
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation