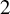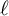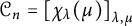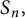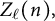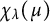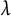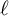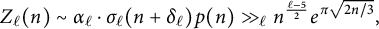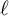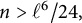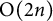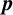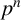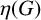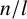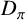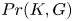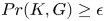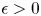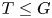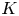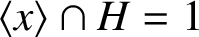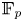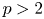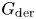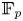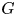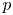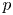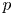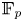Refine listing
Actions for selected content:
616 results in 20Cxx
Quasi-isolated blocks and the Alperin–McKay conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 June 2022, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros in the character tables of symmetric groups with an
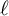 $\ell $-core index
$\ell $-core index
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 27 June 2022, pp. 467-476
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Gelfand–Graev representation of classical groups in terms of Hecke algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1343-1368
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Groups whose Chermak–Delgado lattice is a subgroup lattice of an abelian group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 443-449
- Print publication:
- June 2023
-
- Article
- Export citation
EXTENSION BETWEEN SIMPLE MODULES OF PRO-p-IWAHORI HECKE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 2775-2804
- Print publication:
- November 2023
-
- Article
- Export citation
ON A QUESTION OF MORETÓ
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 306-309
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONJUGACY CLASSES OF MAXIMAL CYCLIC SUBGROUPS AND NILPOTENCE CLASS OF
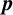 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 463-469
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERSECTION OF CONJUGATE SOLVABLE SUBGROUPS IN FINITE CLASSICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 507-510
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
On finite groups with exactly one vanishing conjugacy class size
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 344-368
- Print publication:
- February 2023
-
- Article
- Export citation
A NOTE ON WIELANDT’S THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 310-314
- Print publication:
- October 2022
-
- Article
- Export citation
GROUPS WITH A GIVEN NUMBER OF NONPOWER SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 315-319
- Print publication:
- October 2022
-
- Article
- Export citation
Invariants for metabelian groups of prime power exponent, colorings, and stairs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 December 2021, pp. 267-297
- Print publication:
- February 2023
-
- Article
- Export citation
PRINCIPAL RADICAL SYSTEMS, LEFSCHETZ PROPERTIES, AND PERFECTION OF SPECHT IDEALS OF TWO-ROWED PARTITIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 690-730
- Print publication:
- September 2022
-
- Article
- Export citation
Corrigendum to ‘Endoscopy for Hecke categories, character sheaves and representations’
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 30 November 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the commuting probability for subgroups of a finite group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 1551-1564
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall-crossings and a categorification of K-theory stable bases of the Springer resolution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2341-2376
- Print publication:
- November 2021
-
- Article
- Export citation
MONOMIAL AND MONOLITHIC CHARACTERS OF FINITE SOLVABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 05 October 2021, pp. 440-448
- Print publication:
- June 2022
-
- Article
- Export citation
ISOLATED SUBGROUPS OF FINITE p-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 449-457
- Print publication:
- June 2022
-
- Article
- Export citation
Unitary representations of type B rational Cherednik algebras and crystal combinatorics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 140-169
- Print publication:
- February 2023
-
- Article
- Export citation
Central elements in affine mod p Hecke algebras via perverse
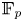 $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2215-2241
- Print publication:
- October 2021
-
- Article
- Export citation