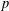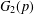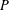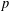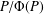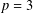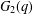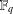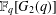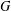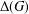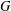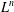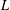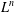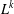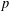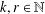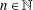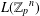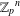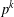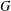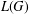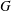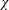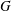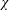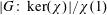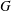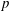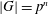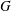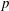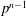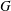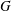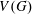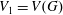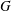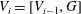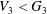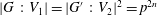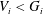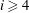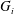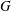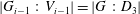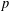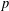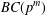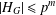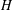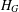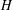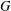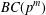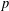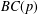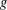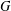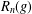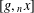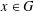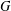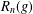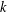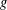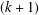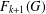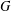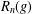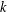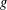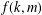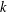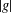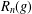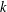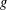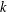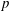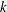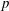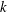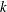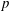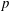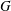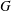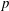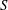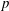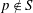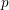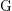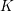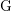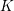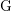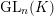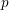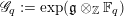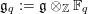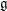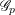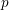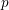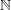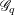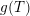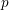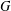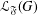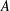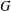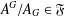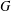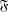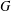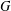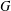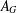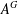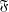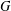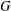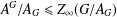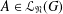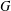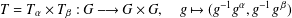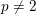Refine listing
Actions for selected content:
616 results in 20Cxx
ON
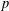 $p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP
$p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP 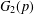 $G_{2}(p)$
$G_{2}(p)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 321-331
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
CHARACTER GRAPHS WITH NONBIPARTITE HAMILTONIAN COMPLEMENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 25 November 2019, pp. 91-95
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A RAMSEY TYPE RESULT FOR LATIN SQUARES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 362-366
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Relative Equivariant Motives and Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 131-159
- Print publication:
- February 2021
-
- Article
- Export citation
Character Codegrees of Maximal Class
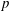 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 25 September 2019, pp. 328-334
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
TAME BLOCK ALGEBRAS OF HECKE ALGEBRAS OF CLASSICAL TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 20 September 2019, pp. 179-201
- Print publication:
- October 2021
-
- Article
- Export citation
FINITE SOLVABLE GROUPS WITH DISTINCT MONOMIAL CHARACTER DEGREES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 04 September 2019, pp. 387-401
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
New Facts about the Vanishing Off Subgroup
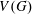 $V(G)$
$V(G)$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 262-268
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
FINITE
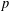 $p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
$p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 255-265
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
RIGHT ENGEL-TYPE SUBGROUPS AND LENGTH PARAMETERS OF FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 340-350
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Retract Rationality and Algebraic Tori
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 173-186
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Kirillov’s orbit method and polynomiality of the faithful dimension of
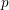 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. 1618-1654
- Print publication:
- August 2019
-
- Article
- Export citation
ON A LATTICE CHARACTERISATION OF FINITE SOLUBLE PST-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 247-254
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CLASSIFICATION OF FINITE GROUPS VIA THEIR BREADTH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 June 2019, pp. 544-563
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
The multistep homology of the simplex and representations of symmetric groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 20 June 2019, pp. 231-253
- Print publication:
- September 2020
-
- Article
- Export citation
ON A PROBLEM OF PRAEGER AND SCHNEIDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 27 May 2019, pp. 80-87
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Permutation groups containing a regular abelian subgroup: the tangled history of two mistakes of Burnside
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 27 May 2019, pp. 613-633
- Print publication:
- May 2020
-
- Article
- Export citation
Robinson’s conjecture on heights of characters
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1098-1117
- Print publication:
- June 2019
-
- Article
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
AN IDENTITY OF PARABOLIC KAZHDAN–LUSZTIG POLYNOMIALS ARISING FROM SQUARE-IRREDUCIBLE MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 April 2019, pp. 81-93
- Print publication:
- February 2021
-
- Article
- Export citation