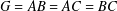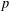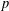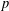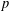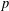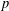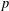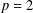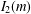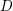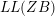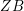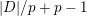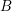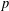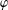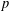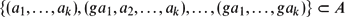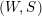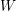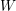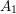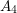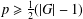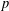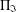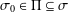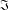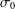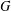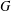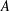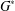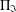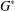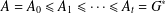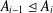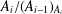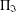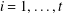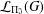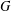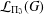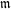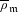Refine listing
Actions for selected content:
616 results in 20Cxx
FINITE TRIFACTORISED GROUPS AND
 $\unicode[STIX]{x1D70B}$ -DECOMPOSABILITY
$\unicode[STIX]{x1D70B}$ -DECOMPOSABILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 31 January 2018, pp. 218-228
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
WEAK CAYLEY TABLE GROUPS OF SOME CRYSTALLOGRAPHIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 635-660
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
FINITE GROUPS WITH ENGEL SINKS OF BOUNDED RANK
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 695-701
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
ON A THEOREM OF KANG AND LIU ON FACTORISED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 54-56
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
GENERATION OF SECOND MAXIMAL SUBGROUPS AND THE EXISTENCE OF SPECIAL PRIMES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 07 November 2017, e25
-
- Article
-
- You have access
- Open access
- Export citation
ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 215-217
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
CLASSIFICATION OF REFLECTION SUBGROUPS MINIMALLY CONTAINING
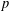 $p$ -SYLOW SUBGROUPS
$p$ -SYLOW SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 57-68
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
The Schwarzian equation for completely replicable functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 20 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 01 October 2017, pp. 30-52
-
- Article
-
- You have access
- Export citation
LOEWY LENGTHS OF CENTERS OF BLOCKS II
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 25 September 2017, pp. 127-138
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
A VARIANT OF HARISH-CHANDRA FUNCTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 14 August 2017, pp. 993-1049
- Print publication:
- September 2019
-
- Article
- Export citation
A spectral incarnation of affine character sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 30 June 2017, pp. 1908-1944
- Print publication:
- September 2017
-
- Article
- Export citation
ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 426-428
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Corners Over Quasirandom Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 6 / November 2017
- Published online by Cambridge University Press:
- 06 June 2017, pp. 944-951
-
- Article
- Export citation
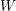 $W$ -GRAPHS AND GYOJA’S
$W$ -GRAPHS AND GYOJA’S 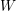 $W$ -GRAPH ALGEBRA
$W$ -GRAPH ALGEBRA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1-43
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
REGULAR ORBITS OF COPRIME LINEAR GROUPS IN LARGE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 438-444
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
ON THE LATTICE OF
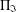 $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$ -SUBNORMAL SUBGROUPS OF A FINITE GROUP
$\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$ -SUBNORMAL SUBGROUPS OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 233-244
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
SUR LA TORSION DANS LA COHOMOLOGIE DES VARIÉTÉS DE SHIMURA DE KOTTWITZ-HARRIS-TAYLOR
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 30 March 2017, pp. 499-517
- Print publication:
- May 2019
-
- Article
- Export citation
Rational Conjugacy of Torsion Units in Integral Group Rings of Non-Solvable Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 813-830
-
- Article
- Export citation
ASYMPTOTIC BOUNDS FOR THE SIZE OF Hom(A, GLn (q))
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 14 March 2017, pp. 51-61
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
FROM COMPLETE TO PARTIAL FLAGS IN GEOMETRIC EXTENSION ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 13 March 2017, pp. 111-121
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation