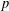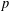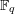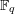Refine listing
Actions for selected content:
616 results in 20Cxx
THE ANNIHILATOR OF TENSOR SPACE IN THE
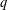 $q$ -ROOK MONOID ALGEBRA
$q$ -ROOK MONOID ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 77-86
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Rings of Polynomials With Artinian Coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 947-954
-
- Article
- Export citation
AN EXPLICIT DIAGONAL RESOLUTION FOR A NON-ABELIAN METACYCLIC GROUP
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 23 March 2017, pp. 499-517
- Print publication:
- 2017
-
- Article
- Export citation
LANDAU’S THEOREM, FIELDS OF VALUES FOR CHARACTERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 December 2016, pp. 37-43
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
SEMIPERMUTABILITY IN GENERALISED SOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 219-227
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
SEMISIMPLICITY OF HECKE AND (WALLED) BRAUER ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1-44
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
SOME INFINITE PERMUTATION GROUPS AND RELATED FINITE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 136-149
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
On the characters of the Sylow
 $p$ -subgroups of untwisted Chevalley groups
$p$ -subgroups of untwisted Chevalley groups 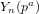 $Y_{n}(p^{a})$
$Y_{n}(p^{a})$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 October 2016, pp. 303-359
-
- Article
-
- You have access
- Export citation
ON THE GENERATING GRAPH OF A SIMPLE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 91-103
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
THE GRADED CENTER OF A TRIANGULATED CATEGORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 74-95
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
GENERALIZED GELFAND–GRAEV REPRESENTATIONS IN SMALL CHARACTERISTICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 09 September 2016, pp. 93-167
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
QUASIRANDOM GROUP ACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 30 August 2016, e24
-
- Article
-
- You have access
- Open access
- Export citation
Character theory approach to Sato–Tate groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 301-314
-
- Article
-
- You have access
- Export citation
ON WEAKLY
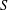 $S$ -PERMUTABLY EMBEDDED SUBGROUPS OF FINITE GROUPS
$S$ -PERMUTABLY EMBEDDED SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 437-448
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
The inverse deformation problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1725-1739
- Print publication:
- August 2016
-
- Article
- Export citation
W-ALGEBRAS FROM HEISENBERG CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 13 July 2016, pp. 981-1017
- Print publication:
- November 2018
-
- Article
- Export citation
THE
 ${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 08 July 2016, e5
-
- Article
-
- You have access
- Open access
- Export citation
Finite Groups and Lie Rings with an Automorphism of Order 2n
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 391-412
-
- Article
- Export citation
A NOTE ON THE
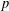 $p$ -SUPERSOLUBILITY OF FINITE GROUPS
$p$ -SUPERSOLUBILITY OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 03 June 2016, pp. 431-436
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Shintani descent for algebraic groups and almost characters of unipotent groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 1697-1724
- Print publication:
- August 2016
-
- Article
- Export citation
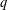
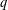
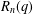
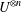
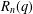
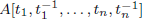 with coefficients in an Artinian ring
with coefficients in an Artinian ring 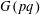
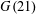
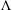
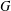
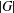
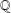
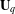
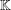
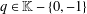
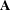
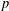
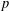
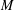

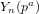
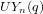

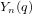

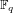


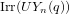
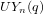
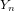
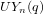


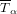
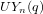
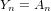
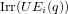
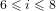
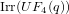
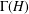
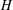
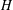
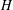
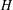
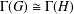
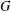
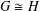
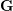
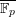
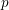
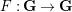
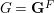
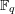

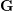
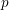
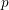
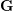
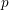
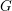
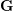
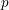
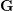
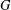
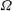
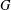
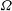
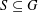
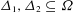
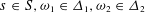
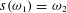
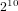
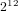
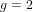
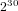
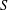
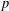
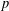
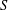
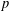
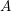
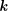

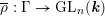
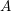
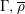
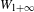
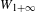
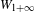

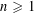
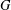
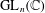
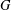
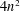
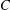
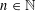
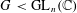
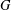
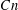

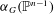
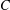
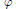 of order 2
of order 2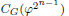 of the involution
of the involution 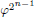 is nilpotent of class
is nilpotent of class 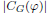 ) be the number of fixed points of
) be the number of fixed points of