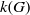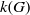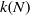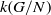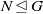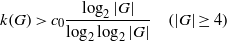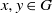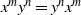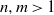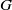Refine listing
Actions for selected content:
616 results in 20Cxx
The Laitinen Conjecture for finite non-solvable groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 303-336
-
- Article
-
- You have access
- Export citation
The string of nets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 223-262
-
- Article
-
- You have access
- Export citation
Matching simple modules of condensation algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 December 2012, pp. 374-384
-
- Article
-
- You have access
- Export citation
AN IDENTIFICATION THEOREM FOR GROUPS WITH SOCLE PSU
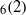 ${}_{6} (2)$
${}_{6} (2)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 25 February 2013, pp. 277-310
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
ON THE EXPONENT OF A VERBAL SUBGROUP IN A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 16 April 2013, pp. 325-332
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Unfaithful minimal Heilbronn characters of L2(q)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 21 November 2012, pp. 57-69
-
- Article
-
- You have access
- Export citation
Supercharacters and pattern subgroups in the upper triangular groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 21 November 2012, pp. 177-186
-
- Article
-
- You have access
- Export citation
The centralizer of a subgroup in a group algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 20 November 2012, pp. 49-56
-
- Article
-
- You have access
- Export citation
Sparse fusion systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 19 November 2012, pp. 135-150
-
- Article
-
- You have access
- Export citation
On primordial groups for the Green ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 24 October 2012, pp. 337-347
-
- Article
-
- You have access
- Export citation
A pair of characteristic subgroups for pushing-up. II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 24 October 2012, pp. 71-133
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF NONINNER AUTOMORPHISMS OF ORDER TWO IN FINITE 2-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 17 September 2012, pp. 278-287
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
EXISTENCE OF NONINNER AUTOMORPHISMS OF ORDER p IN SOME FINITE p-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 17 September 2012, pp. 272-277
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
NEW REDUCTIONS AND LOGARITHMIC LOWER BOUNDS FOR THE NUMBER OF CONJUGACY CLASSES IN FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 07 September 2012, pp. 406-424
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Finite p-solvable groups with three p-regular conjugacy class sizes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 371-386
-
- Article
-
- You have access
- Export citation
Cohomological uniqueness of some p-groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 449-468
-
- Article
-
- You have access
- Export citation
THE PROBABILITY THAT
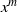 $\lowercase {X}^{\lowercase {M}}$ AND
$\lowercase {X}^{\lowercase {M}}$ AND 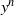 $\lowercase {Y}^{\lowercase {N}}$ COMMUTE IN A COMPACT GROUP
$\lowercase {Y}^{\lowercase {N}}$ COMMUTE IN A COMPACT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 503-513
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Computing Hall subgroups of finite groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 205-218
-
- Article
-
- You have access
- Export citation
The Brauer characters of the sporadic simple Harada–Norton group and its automorphism group in characteristics 2 and 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 257-280
-
- Article
-
- You have access
- Export citation
PyCox: computing with (finite) Coxeter groups and Iwahori–Hecke algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 231-256
-
- Article
-
- You have access
- Export citation
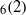
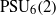
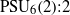
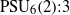
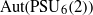
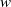

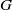
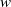

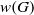

 with
with